Abstract: A project on the use of random processes in a musical context. Basically, two different models are used. These generate chord sequences, which are then provided with a rhythm and an overlying melody.
Responsible: Moritz Reiser
Overview
The overall structure of the program, which corresponds to the content of the main patch, can be seen in Figure 1. At the top is the selection of the algorithm to be used for chord progression generation. This can be selected via the selection field at the top left. The two input fields of the subpatches can be used to specify the desired length and the starting chord or the key of the composition.
This is followed by a random determination of the respective tone lengths. Here you can set the tempo in BPM as well as the frequencies of the tone lengths occurring in multiples of quarter notes. The respective start times of the chords are calculated from the calculated durations using a “dx→x” function. When using the program, care must be taken here that Open Music calculates new random numbers in both strings due to the output being used twice, as a result of which the relationship between the start time and the tone duration is lost. This can be remedied by locking the subpatches for chord progression and tone length generation with “Lock Eval” after running the program once and then running it again to adjust the start times to the now saved tone durations (see information panel in the main patch). The third major step in the overall process is the generation of a melody that lies above the chord sequence. Here, a note is selected from the underlying chord and shifted up an octave. You can set whether this should always be a random chord tone or whether the tone closest to or furthest away from the preceding melody tone should be selected.
The result is then visualized at the bottom in a multi-seq object.
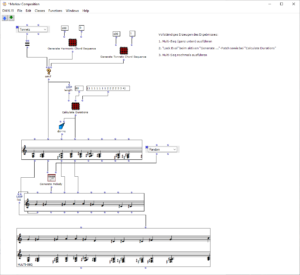
Figure 1: Overall structure of the composition process
Chord progression generation
Two algorithms are available for generating the chord sequence. The desired length of the sequence, which corresponds to the number of chords, and the starting chord or the key are transferred to them.
Harmonic chord sequence using Markov chain
The sequence of the first algorithm can be seen in Figure 2. The subpatch “Create Harmonic Chords” generates the basic set of chords that will be used in the following. This corresponds to the usual levels of counterpoint theory and, in addition to the tonic, subdominant, dominant and their parallels, contains a diminished chord on the seventh degree, a sixth ajoutée of the subdominant and a dominant seventh chord. The “Key” input adds a value corresponding to the desired key to these chords.
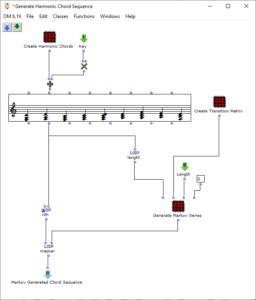
Figure 2: Subpatch for generating a harmonic chord sequence using a Markov chain
The “Create Transition Matrix” subpatch generates a matrix with transition probabilities for the individual chords. For each chord step, the probability with which it transitions to a certain other chord is determined. The probability values were chosen arbitrarily according to the usual processes in counterpoint theory and adjusted experimentally. For each chord it was investigated how likely it is to transition from this chord to another chord, so that the result corresponds to the conventions of counterpoint theory and allows a frequent return to the tonic level in order to focus on it. The exact transition probabilities are listed in the following table, whereby the initial sounds are listed in the left-hand column and the transitions are represented line by line.
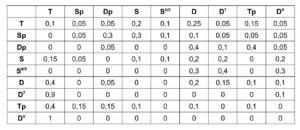
Table 1. Transition probabilities of the harmonies of corresponding chord levels
The generation of the chord sequence finally takes place in the patch “Generate Markov Series”, which is shown in Figure 3. This initially only works with the numbering of the chord steps, which is why it is sufficient to pass it the length of the chord list. The Lisp function “Markov Synthesis” now generates a chord sequence of the desired length using the transition matrix. As it is not guaranteed that the last chord in the sequence generated in this way corresponds to the tonic, another Lisp function is used, which generates further chords until the tonic is reached. As the steps have only been numbered so far, the chords valid for the respective steps are finally selected in order to obtain the finished chord sequence.
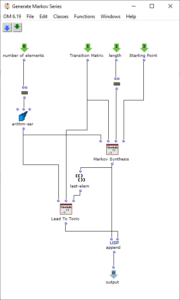
Figure 3: Subpatch for generating a chord sequence using Markov synthesis
Chromatic chord progression using a tone net
In contrast to the harmonic chord progression, all 24 major and minor chords of the chromatic scale are used here (see Figure 4). The special feature of this algorithm lies in the choice of transition probabilities. These are based on a so-called tone network, which is shown in Figure 5.
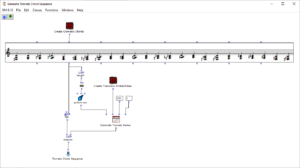
Figure 4: Subpatch for generating a chord sequence based on the tone net representation

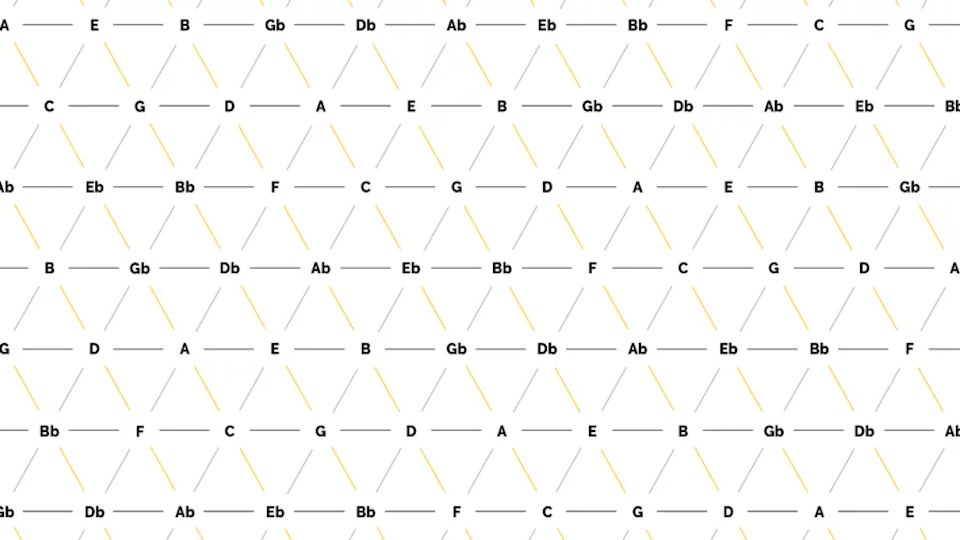
Figure 5: Tonnetz (image source:<https://jazz-library.com/articles/tonnetz/>)
Within the tone net, individual tones are applied and connected to each other. On the horizontal lines, the tones are each a fifth apart, while the diagonal lines show minor thirds (from top left to bottom right) and major thirds (from bottom left to top right). The resulting triangles each represent a triad, for example the triangle of the notes C, E and G results in the chord C major. All major and minor chords of the chromatic scale can be found. The Tonnetz representation is mostly used for analysis purposes, as a Tonnetz allows you to see directly how many tones two different triads share. One example is the analysis of classical music of the romantic and modern periods as well as film music, as the harmonic counterpoint rules used above are often neglected here in favor of chromatic and other previously unusual transitions. The distance between two chords in the tonal network can be a measure of whether the transition of one chord into the other is melodious or rather unusual. It is calculated from the number of edges that have to be crossed to get from one chord triangle to another. In other words, it corresponds to the degree of adjacency between two triangles, whereby a direct adjacency results from sharing an edge. Figure 6 shows an example of this: To get from the chord C major to the chord F minor, three edges have to be crossed, resulting in a distance of 3.
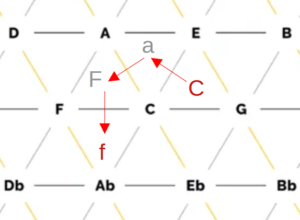
Figure 6: Example of determining the distance in the tone network using the transition from C major to F minor
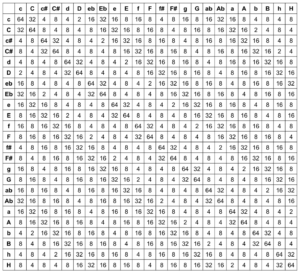
As part of the project, the transition probabilities are now calculated on the basis of the distances between chords in the tone network. It is only necessary to distinguish whether the active triad is a major or minor chord, as the same distances to other chords result for all keys within these two classes. This means that every transition can be calculated from C major or C minor and then shifted to the desired key by adding a value. Starting from both variants (C major and C minor), the distances to all other triads were first recorded in the tonal network:
Distances from C major:

Intervals from C minor:

In order to obtain probabilities from the intervals, all values were first subtracted from 6 to make larger intervals less probable. The results were then used as the exponent of the number 2 in order to give greater weighting to closer chords. Overall, this results in the formula
P=2^(6-x) ; P=probability, x=distance in the grid
to calculate the transition weights. These result in the following matrix for all possible chord combinations, from which 342 probabilities result when divided by the row sum.
Within the patch, the Lisp function “Generate Tonnetz Series” first determines whether the active chord is a major or minor triad. As with the harmonic procedure, only the numbers 0-23 are used initially, this can be determined using a simple modulo-2 calculation. Depending on the result, the respective probability vector is used, a new chord is determined and finally the previous step is added. If the result is a number greater than 23, 24 is subtracted in order to always remain within the same octave.
After the previously determined length of the sequence, this section is finished. There is no return to the tonic as in the previous section, as the chromaticism means that the tonic is not as pronounced as in the harmonic chord sequence.
Determining the tone lengths
After a chord progression has been generated, random lengths are calculated for the individual triads. This is done in the “Calculate Durations” subpatch, which is shown in Figure 6. In addition to the desired BPM number, a list of note lengths is transferred as multiples of quarter notes. More probable values occur more frequently in this pool, so that a corresponding selection can be made via “nth-random”.
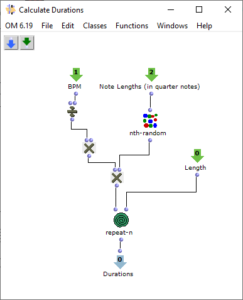
Figure 7: Subpatch for random determination of note durations
Melody generation
The basic melody generation process has already been described above: A tone is selected from the respective chord and transposed up an octave. This tone can be selected at random or according to the smallest or largest distance to the previous tone.
Sound examples
Example of a harmonic chord sequence:
Example of a tone net chord sequence: