Abstract: OpenMusic und die Bibliothek OM-SoX wurden genutzt, um eine Möglichkeit zu schaffen, Mono-Audiodateien als 3D-Ambisonics-Signal bis zur dritten Ordnung zu kodieren.

Verantwortlicher: Alexander Nguyen (WS 2023/24)

Haupttext:

** UPDATE (April 2025) ** Die Implementierung wurde überarbeitet. Der Encoder ist nun als OM-SoX-Klasse nutzbar und unterstützt Encoding bis zur siebten Ordnung! Für mehr Informationen, siehe https://git.marlonschumacher.de/summary/?r=Spatial/OM-SoX_hoaencode.git

Ambisonics

Ambisonics ist ein Verfahren, um ein zwei- oder dreidimensionales Klangfeld (soundfield) zu beschreiben (im Folgenden beschränke ich mich auf 3D-Ambisonics). Bei Ambisonics wird eine Basis von orthogonal zueinanderstehenden Funktionen und das sphärische Koordinatensystem genutzt, um das von einer Schallquelle resultierende Klangfeld entlang einer Kugeloberfläche zu beschreiben. Der einfachste Fall ist „Zero-th Order Ambisonics“, das einem idealen, omnidirektionalen Mikrofon gleicht: es wird genau ein Audiokanal genutzt (auch „W“-Kanal genannt, laut Furse-Malham-Bezeichnung). Bei „First Order Ambisonics“ (FOA) wird das Signal auf zusätzliche drei Kanäle (drei Basen) aufgeteilt: Es sind die drei „Richtungs“komponenten (auch genannt X, Y, Z-Kanal). Angenommen, eine ideale Punkt-Schallquelle ist am Ende einer dieser Achsen platziert, dann wird auch nur auf dieser Achse (derselben Ordnungszahl) das Signal enthalten sein. Im Fall von Ambisonics werden immer auch die Kanäle niedrigerer Ordnungen mitgegeben, d.h. das FOA-Signal besteht aus insgesamt vier Audiokanälen. Im Allgemeinen kann die Anzahl der Kanäle für ein 3D-Ambisonics-Signal $n$-ter Ordnung berechnet werden anhand der Formel $(n+1)^2$ (das heißt, bei n=0: 1; bei n=1: 4, bei n=2: 9, bei n=3: 16). Ambisonics-Signale mit ‚höheren‘ Ordnungszahlen (…, 2, 3, 4, …) werden auch als Higher Order Ambisonics (HOA) bezeichnet.

Channel Numbering

Ein HOA-Signal besteht also aus mehreren Komponenten. Es gibt mehrere Ansätze, die Komponenten in einer Mehrkanal-Audiodatei zu sortieren. Die hier für dieses Projekt gewählte Sortierung ist das „Ambisonic Channel Number“ing (ACN), bei der jedem Kanal eine ganzzahlige Nummer beginnend bei Null (0) zugewiesen wird. Der erste Kanal trägt also die Bezeichnung „0“, der zweite Kanal „1“, der dritte Kanal „2“ usw. Anhand dieser numerischen Bezeichnung kann die ‚Ordnung‘ (order) l und der ‚Grad‘ (degree) m, zu der die Komponente gehört, ermittelt werden. Siehe Tabelle 1 für eine Übersicht über alle Komponenten von 3rd Order Ambisonics (3OA) – und eine Kollationierung mit einer alternativen Bezeichnung, „Furse Malham“ (FuMa).

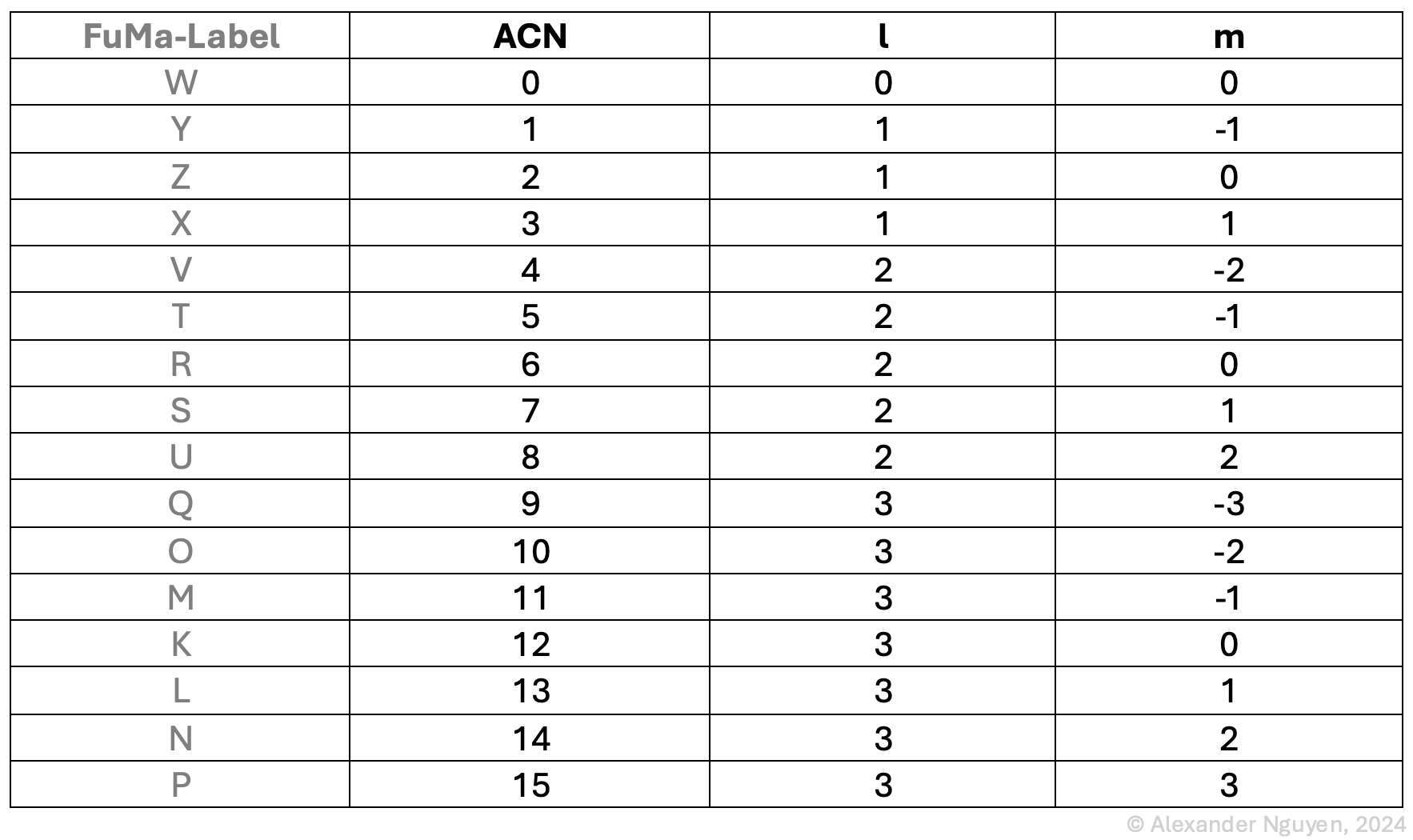
Tabelle 1. Auswertung der Formeln für l und m anhand der ACN-Werte. Zusätzlich die alternative Bezeichnung nach Furse-Malham (FuMa).

Normalization

Die Werte  (Order) und  (Degree) werden genutzt, um einen Normalisierungsfaktor für jeden Audiokanal zu berechnen. Die hier gewählte Normalisierung heißt “Semi-Normalized 3D” (SN3D). Siehe Tabelle 2 für eine Übersicht über die Normalisierungsfaktoren für alle Komponenten von 3rd Order Ambisonics.

ACN-Sortierung zusammen mit SN3D-Normalisierung spiegeln eine derzeit geläufige Konvention namens ambiX (Nachbar et al., 2011) wider.

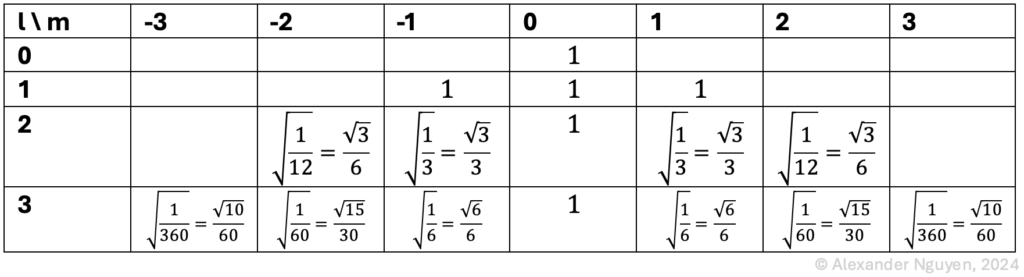
Tabelle 2. SN3D-Faktoren für Order l und Degree m, d.h. N_lm^((SN3D)). Hinweis: Wenn also m=0 ist, ist auch immer N_l0^((SN3D) )=1, und die Tabelle ist symmetrisch bezüglich m.

Encoding

Um eine Punktschallquelle in Ambisonics abzubilden, addiert man dessen Audiosignal auf jeden der  Audiokanäle, gewichtet anhand des eben beschriebenen Normalisierungsfaktors und eines Dämpfungsfaktors. Dieser Dämpfungsfaktor ist abhängig vom Einfallswinkel (beschrieben im sphärischen Koordinatensystem) und der ACN-Nummer (d.h. Ordnung  und Grad ). Eine Intuition anhand von FOA: Die Dämpfung ist minimal (0 dB bzw. Faktor 1), wenn der Einfallswinkel mit einer der Achsen (x, y oder z) zusammenfällt, maximal (–∞ dB bzw. Faktor 0), wenn sie senkrecht zu dieser steht.

In Ambisonics wird das 3D-Koordinatensystem üblicherweise so definiert: Als „vorne“ (aus Hörer*innen-Sicht) definiert man die positive x-Achse. Das heißt, die positive y-Achse zeigt nach „links“ und die positive z-Achse zeigt nach „oben“. Für die Transformation zu Polarkoordinaten, d.h. zum sphärischen Koordinatensystem, definiert man dabei 0° Azimut () koinzident zur positiven x-Achse auf der xy-Ebene, linksdrehend. 0° Elevation () koinzident zur xy-Ebene, maximal positiv, wenn koinzident zur positiven z-Achse (siehe Abbildung 1), wobei gilt: 0≤θ≤2π,
-π/2≤ϕ≤π/2.

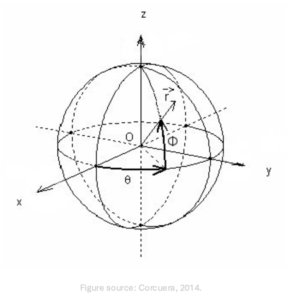
Abbildung 1. Visualisierung des Koordinatensystems und der Bezugspunkte. Positiv-x = vorne, positiv-y = links, positiv-z = oben. θ (theta) linksdrehend (0° = vorne), ϕ „aufwärtsdrehend“ (0° = in der xy-Ebene).

Um nun das zeitabhängige Signal $S(t)$  einer Punktschallquelle mit Einfallswinkeln $θ, ϕ$ in Ambisonics zu encodieren, wird der Signalanteil für jeden Ambisonics-Kanal $B_l^m$ eigens berechnet. Dazu wird das Signal mit einem Dämpfungsfaktor $Y_l^m$ multipliziert:

Die Formel für den Dämpfungsfaktor lautet (siehe Nachbar et al., 2011):

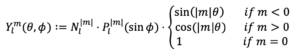
wobei $P_l^m$ das „assoziierte Legendre-Polynom“ $l$-ter Ordnung und $m$-ten Grades ist, und $P_l$ das (unassoziierte) Legendre-Polynom $l$-ter Ordnung (in der Rodrigues-Darstellung). Diese sind wie folgt definiert:

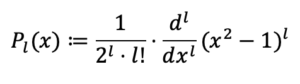
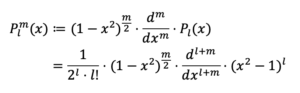
Zum Beispiel:

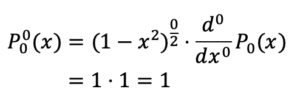
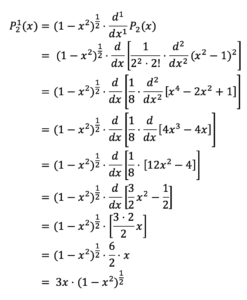
Setzt man nun $x≡sin⁡(ϕ)$ setzt, erhält man eine der Spherical Harmonics (siehe Tabelle 3 für weitere Beispiele):

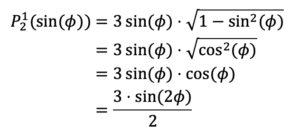
Für FOA lauten die Formeln also:

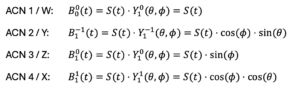
Tabelle 3. Ambisonics-Formeln bis zur dritten Ordnung (ACN-Zählung, SN3D-Normalisierung, 0≤θ≤2π Azimut (0° = vorne, linksdrehend), -π/2≤ϕ≤π/2 Elevation (0° = auf der xy-Ebene, aufwärtsdrehend)).

Entwurf einer OM-SoX Implementierung

Im Rahmen dieses Projekts wurde eine Implementierung in OpenMusic (v7.3) mit der Bibliothek OM-SoX (v1.0.1) angefertigt (getestet unter macOS 14.5).

Die Signalverarbeitung besteht aus folgenden Schritten:

1. 1. Gegeben sei das Mono-Signal einer Audiodatei, Azimut $θ$, Elevation $ϕ$ und die Ambisonics-Order $L$.
   2. Berechne die Dämpfungsfaktoren $Y_l^m (θ,ϕ) $ für alle Ordnungen $0≤l≤L$.
   3. Erstelle eine Multi-Channel-Audiodatei mit $n_channels ≔ (l+1)^2$ Audiokanälen.
   4. Jeder Kanal $ch$, $0≤ch≤n_channels$, entspricht dabei dem Signal $S(t)$, multipliziert mit dem entsprechenden Dämpfungsfaktor und Normalisierungsfaktor.

Im Falle von mehreren Audio-Dateien werden diese einfach kanalweise addiert.

In OpenMusic wurden hierfür folgende Haupt-Funktionen (in Form von Patches) definiert:

• • ambisonics-gains
    Gegeben eine (maximale) Order werden die Dämpfungsfaktoren berechnet.
  • ambisonics-encoder_simple
    Gegeben eine Audiodatei, Azimut, Elevation und Order wird eine Multichannel-Audiodatei generiert und zurückgegeben.
  • ambisonics-encoder
    Gegeben eine Liste von Audiodateien (selbst wenn nur eine Audiodatei) und entweder a) eine Liste von Azimut-Elevation-Tupeln, oder b) eine Liste von xyz-Tupeln, oder c) ein 3dc-Objekt (mit entsprechend vielen Koordinaten) wird eine Multichannel-Audiodatei generiert und zurückgegeben.

Folgende Hilfs-Funktionen werden definiert.

• • deg-to-rad
    Gegeben eine Zahl in Grad wird das Bogenmaß zurückgegeben. Diese Funktion nutzt double-precision floats, insbesondere um für die Berechnungen mit den trigonometrischen Funktionen bei hoaenc.ambisonics-gains ausreichend präzise zu sein. Hinweis: Für die Signalverarbeitung mit OM-SoX können keine double-precision floats benutzt werden; die berechneten Gain-Werte werden dafür wieder zu single-precision floats konvertiert.
  • 3dc-to-spherical
    Gegeben ein 3dc-Objekt werden Azimut-Elevation-Tupel berechnet und zurückgegeben. Das Koordinatensystem ist: 0° Azimut = positive x-Achse, 90° Azimut = positive y-Achse, 90° Elevation = positive z-Achse, 0° Elevation = xy-Ebene.
  • 3dc-translate
    Gegeben ein 3dc-Objekt und ein xyz-Tupel wird der Ursprung des Koordinatensystems um den gegebenen Wert verschoben. Eine Koordinate (1 1 0) wird bei Verschiebung um (1 1 0) also zu (0 0 0).
  • 3dc-rotate
    Gegeben ein 3dc-Objekt und ein ypr-Tupel (yaw, pitch, roll) wird das Koordinatensystem um yaw entlang der z-Achse rotiert, um pitch entlang der y-Achse und um roll entlang der x-Achse. Wenn man sich ein Flugzeugmodell vorstellt, mit der Spitze entlang der positiven x-Achse und dem linken Flügel entlang der positiven y-Achse, dann entspricht positiv-yaw einer Rotation der Spitze entlang des Horizontes nach rechts, positiv-pitch einem Anheben der Spitze und positiv-roll einem Anheben des linken Flügels.

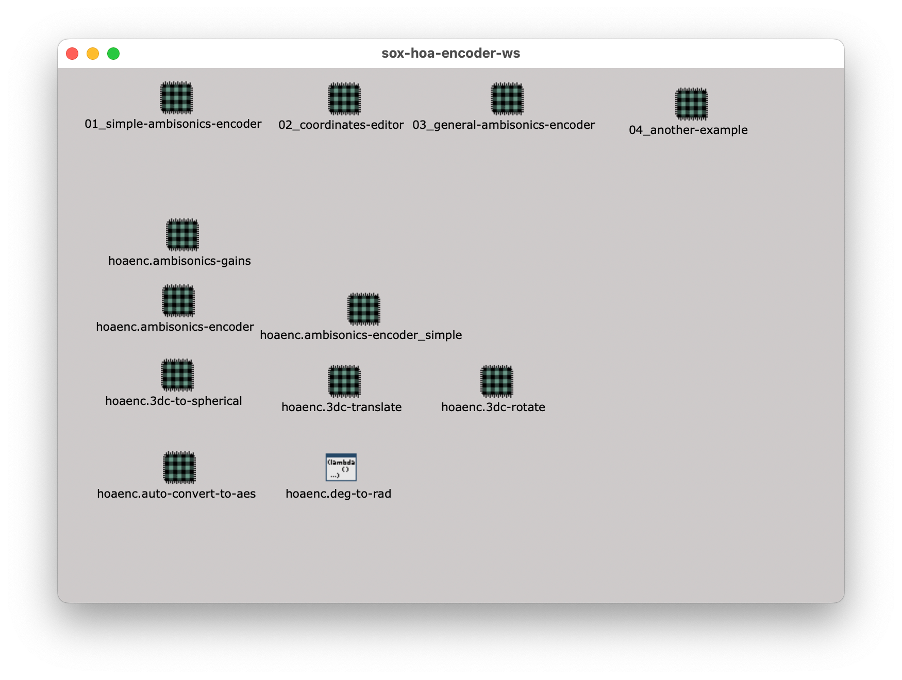
Screenshot vom Projekt-Workspace der hier vorgestellten Implementierung eines HOA-Encoders in OpenMusic. Oben: Beispiele, unten: einzelne Funktionen des HOA-Encoders.

Beispiel

Im folgenden Beispiel werden zwei Audio-Dateien (amen-break.wav und noise-white.aif) zu einem HOA-Signal 3. Ordnung transformiert. Den Audio-Dateien werden zwei verschiedene Positionen anhand einer Liste mit XYZ-Koordinaten zugewiesen. Diese Koordinaten werden in einem 3DC-Objekt gespeichert und noch um -30° entlang der Roll-Achse rotiert, d.h. entlang der positiven x-Achse („vorne“) schauend wird die linke Seite nach unten bewegt. Anschließend werden die Schallquellen um -1.5 Einheiten entlang der y-Achse verschoben, d.h. um 1.5 nach rechts (unter Beibehaltung der „Blickrichtung“).

Zu hören ist: Amen Break-Signal links, Rausch-Signal links vorne.

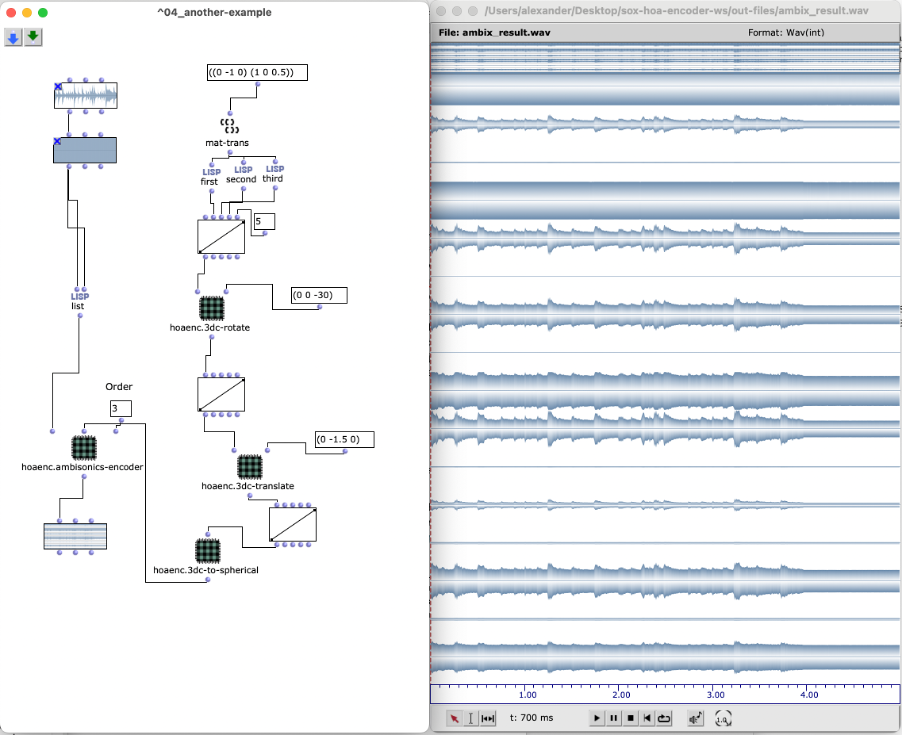
Audio 1: amen-break.wav

Zusammenfassung

Im Rahmen dieses Projektes wurde recherchiert, wie die Ambisonics-Formeln dargestellt werden können. Mit diesem Wissen wurden die benötigten Dämpfungsfaktoren für 3D-Ambisonics bis zur dritten Ordnung hergeleitet (unter Einhaltung der ambiX-Konvention (Nachbar et al., 2011), d.h. ACN-Sortierung und SN3D-Normalisierung. In OpenMusic wurden Funktionen geschrieben, um (im einfachen Fall) eine Mono-Schallquelle für Ambisonics 0., 1., 2. und 3. Ordnung und (im allgemeinen Fall) eine beliebige Anzahl von Mono-Schallquellen zu kodieren. Im allgemeinen Fall ist es möglich, entweder xyz-Koordinaten, Azimut-Elevation-Koordinaten oder sogar ein 3DC-Objekt anzugeben. Es wurden Funktionen geschrieben, um das Koordinatensystem des 3DC-Objekt zu transformieren (konkret: zu verschieben oder zu rotieren). Es wurden Beispiele angefertigt, die den funktionalen Gebrauch zeigen.

© Alexander Nguyen, 2024.

Referenzen

Corcuera Marruffo, Andrea. “A Real-Time Encoding Tool for Higher Order Ambisonics,” December 5, 2014. http://repositori.upf.edu/handle/10230/22890.

Nachbar, Christian, Franz Zotter, Etienne Deleflie, and Alois Sontacchi. “AMBIX – A SUGGESTED AMBISONICS FORMAT” [with comments from 2016], Lexington, KY, 2011. https://ambisonics.iem.at/proceedings-of-the-ambisonics-symposium-2011/ambix-a-suggested-ambisonics-format.

Außerdem: ambisonics.ch (via archive.org), Wolfram MathWorld, Wikipedia.