Schlagwort-Archiv OpenMusic

  • Home   /  
  • Markierte Beiträge "OpenMusic"
VonLukas Körfer
, , ,

Wellenfeldsynthese mit OM-SoX

Abstract: Dieses Abschlussprojekt entstand zum Ende des Wintersemesters 2023/24 im Rahmen der Lehrveranstaltung „Symbolische Klangverarbeitung und Analyse/Synthese“ des MA Musikinformatik. Hierbei wurde in dem Programm OpenMusic mithilfe der Library OM-SoX und des Verfahrens der Wellenfeldsynthese eine Anwendung zur Klangverräumlichung erarbeitet. 

Verantwortliche: Lukas Körfer

Wellenfeldsynthese

Bei der Wellenfeldsynthese (kurz: WFS) handelt es sich um das Verräumlichen von virtuellen Klangquellen mithilfe eines Loudspeaker-Arrays. Bei dieser fortschrittlichen Audiotechnologie wird also versucht, Klänge so zu reproduzieren, dass sie den Eindruck erwecken, dass sie von einer bestimmten Position im Raum kommen. Das gelingt durch die Erzeugung eines Wellenfeldes, welches aus einer Vielzahl von einzelnen Schallquellen besteht, die in einer Art synchronisiert werden, so dass eine kohärente Schallwelle entsteht, mit welcher es möglich sein soll, eine virtuelle Klangquelle im Raum lokalisieren zu können. 

 

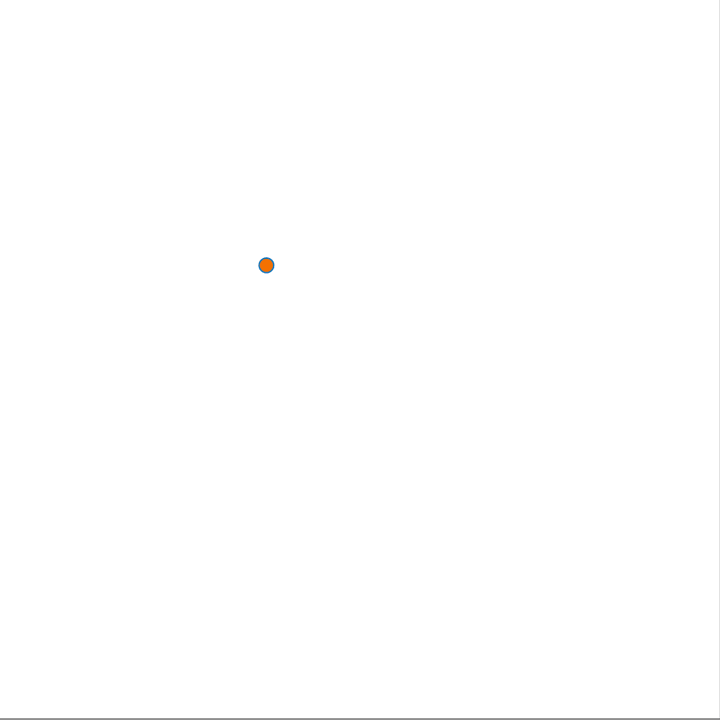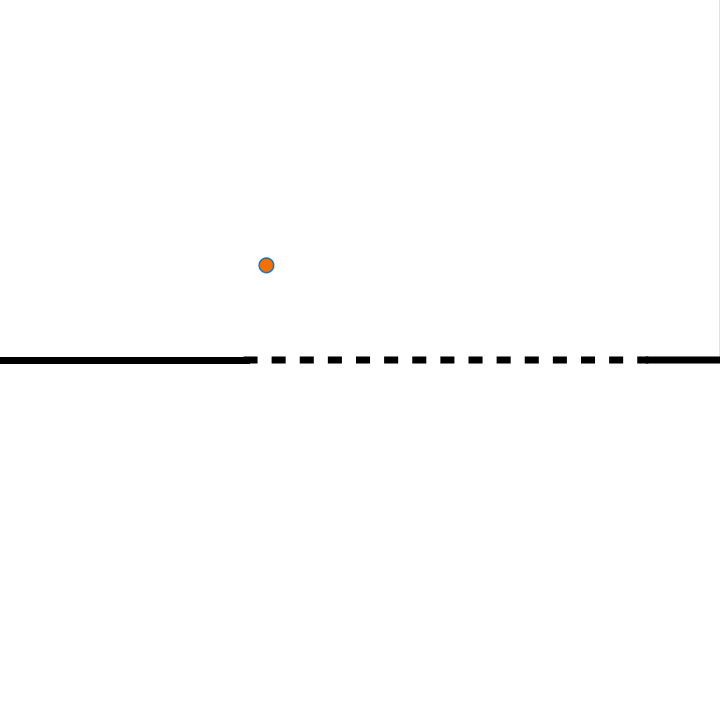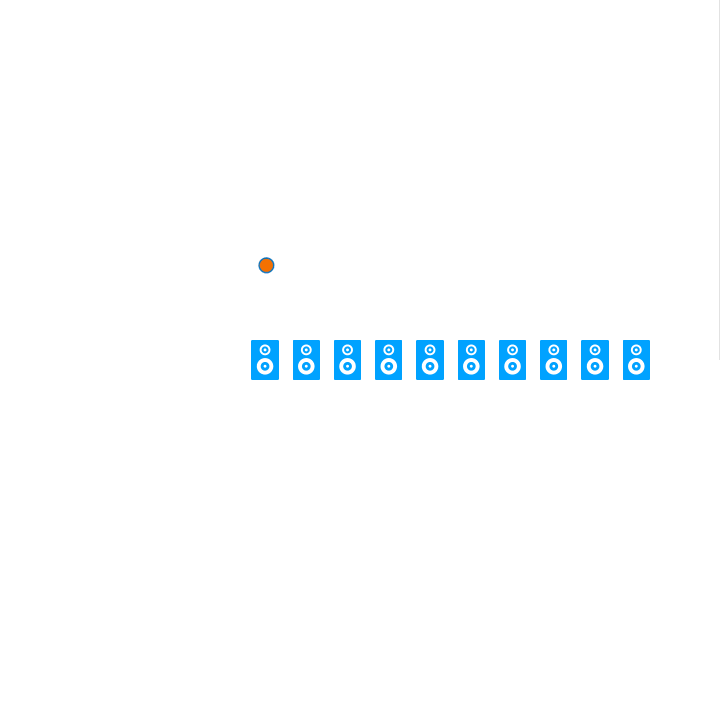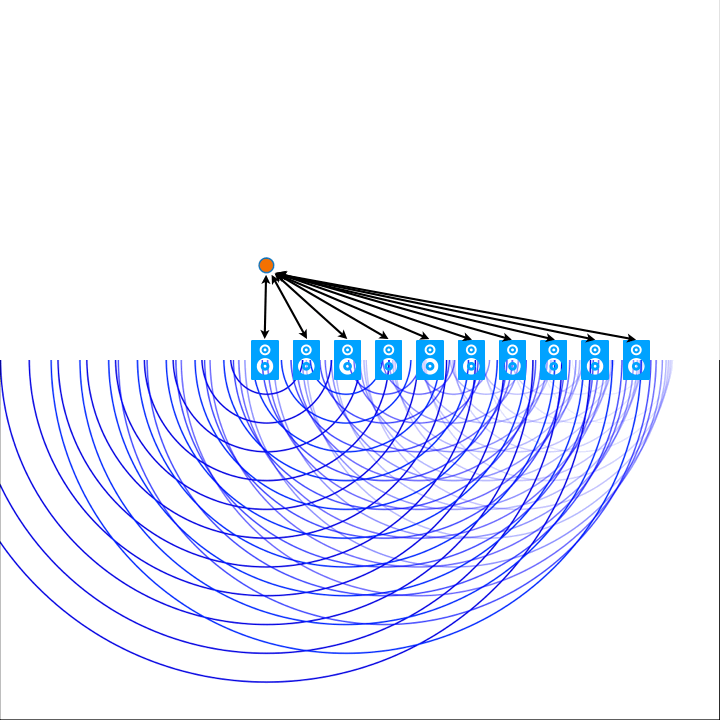
Zum besseren Verständnis der Funktionsweise von WFS kann man sich dem Thema über das physikalische Phänomen von Interferenzmusterbildung hinter einem Hindernis mit Öffnungen nähern. Wenn eine Welle auf einen oder mehrere Schlitze trifft, wird sie durch die Öffnungen hindurchgebeugt und breitet sich hinter dem Hindernis aus. Dies führt zur Bildung eines Musters von Welleninterferenz auf der anderen Seite des Hindernisses. In ähnlicher Weise nutzt die Wellenfeldsynthese ein Array von Lautsprechern, um eine kohärente Schallwelle zu erzeugen. Dafür muss eine präzise Berechnung und Steuerung der Phasen- und Amplitudenverhältnisse der Schallwellen, die von jedem einzelnen Lautsprecher ausgehen, vorgenommen werden. Diese Berechnungen sind abhängig von den Abständen jedes einzelnen Lautsprechers im Array relativ zur Position im Raum der jeweiligen virtuellen Klangquelle. 

Projektbeschreibung

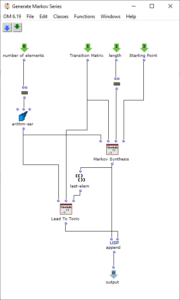
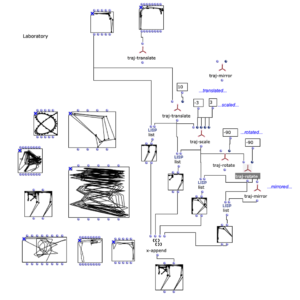
Für dieses Projekt sollte nun ein Programm entstehen, mit dem allgemeinen Ziel, durch gewissen Einfluss und Anpassungen eines Anwenders letztendlich eine Mehrkanal-Audiodatei zu erhalten, die zur Wellenfeldsynthese mit einem Loudspeaker-Array verwendet werden kann. Dafür musste zunächst konzipiert werden, welche Parameter vom Anwender des Programms gesetzt und beeinflusst werden sollen.

User-Input

 

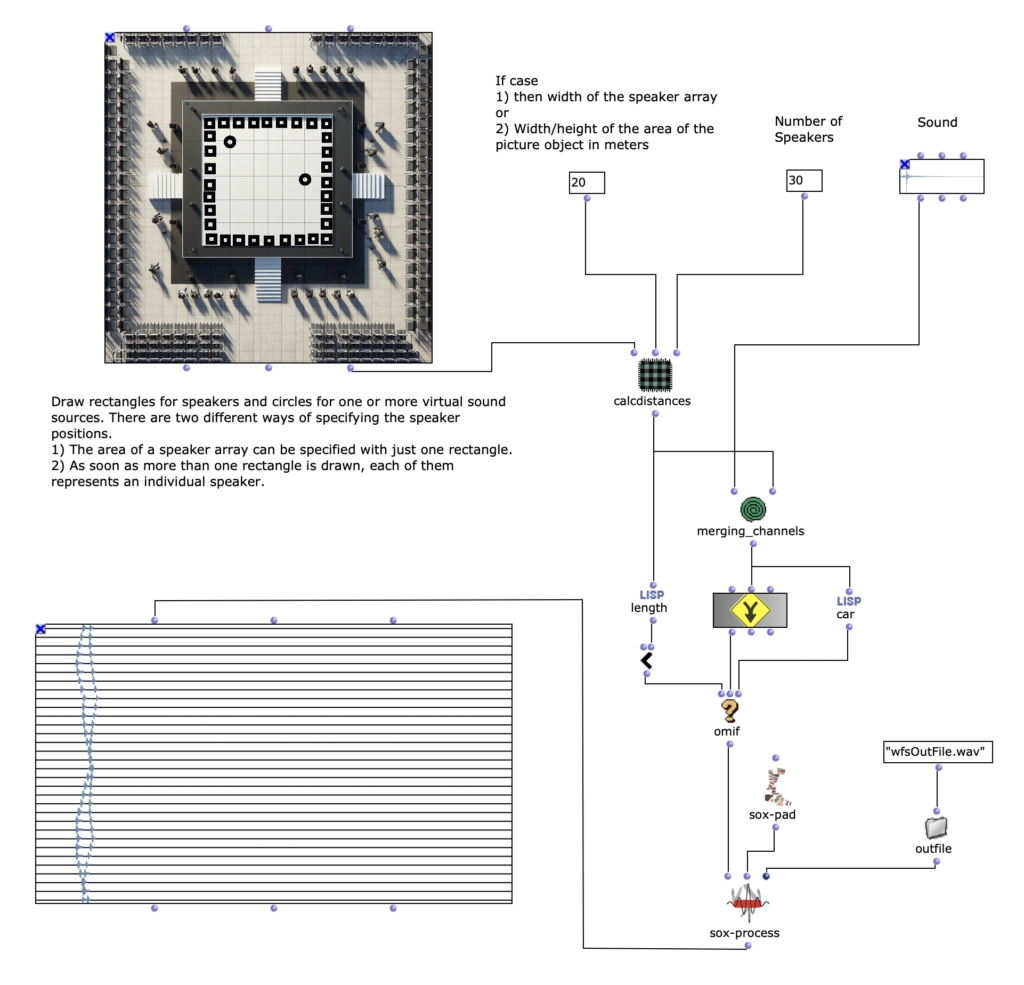
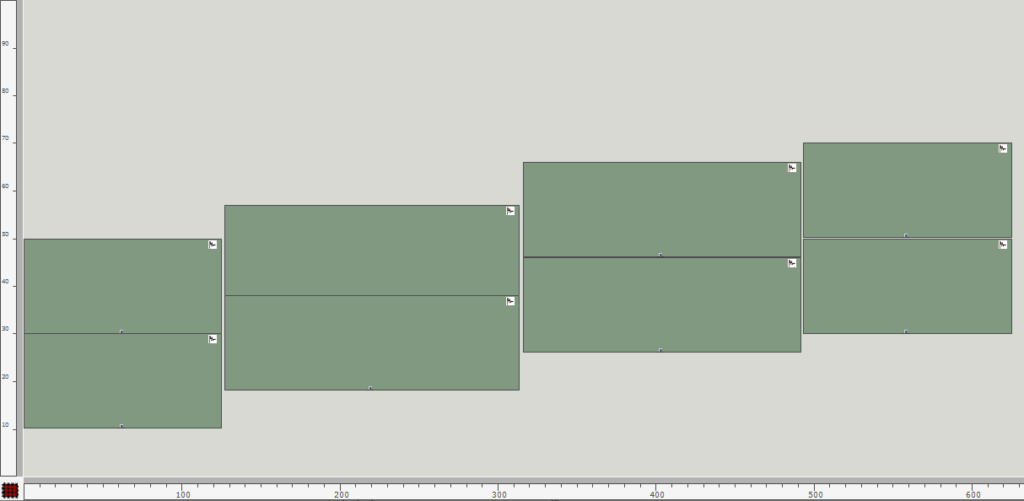
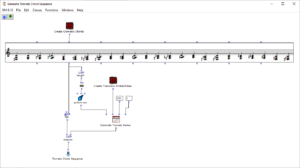
Neben der Audiofile, welche zur Verräumlichung verwendet werden sollte, muss durch den Anwender einerseits gewisse Angaben zum Loudspeaker-Array und andererseits die Position oder Positionen einer oder mehrerer virtueller Klangquellen relativ zum Loudspeaker-Array angegeben werden. Um eine möglichst einfache und intuitive Konfiguration des Programms zu ermöglichen, habe ich mich dazu entschieden, dafür hauptsächlich ein Picture-Objekt zu verwenden, in welchem der Aufbau aufgezeichnet werden kann. Durch das Zeichnen eines Rechtecks können die Positionen der Loudspeaker und mit Kreisen die der virtuellen Klangquellen angegeben werden. Es kann dabei ein oder mehrere Kreise gezeichnet werden, wobei jeder Kreis eine Klangquelle repräsentiert. Die Angabe der Loudspeaker ist durch zwei unterschiedliche Weisen möglich. Wenn nur ein einziges Rechteck im Picture-Objekt gezeichnet ist, so stellt dieses den Bereich eines Loudspeaker-Arrays dar. Um im nächsten Schritt des Programms die konkreten Positionen der einzelnen Loudspeaker ermitteln zu können, sind ihr zusätzlich noch zwei weitere Angaben nötig. Das ist zum einen die Länge des Loudspeaker-Arrays in Metern; damit wird gleichzeitig der Maßstab für den kompletten gezeichneten Aufbau beeinflusst. Und zum anderen muss die Anzahl der Loudspeaker im gezeichneten Bereich angegeben werden. Sobald mehr als ein Rechteck vom Anwender angegeben sind, steht jedes einzelne Rechteck für einen individuellen Loudspeaker. Um bei dieser Variante einen Maßstab für den gezeichneten Aufbau festlegen zu können – was vorher mit der Angabe der Länge des Loudspeaker-Arrays möglich war – kann nun die Breite / Höhe vom Bereich des kompletten Picture-Objekts angegeben werden. Mit der ersten Variante, dass das Loudspeaker-Array lediglich mit einem Rechteck gezeichnet werden kann, wird zwar die Anwendung deutlich unkomplizierter, setzt allerdings auch voraus, dass die Loudspeaker linear und mit einem gleichmäßigen Abstand zueinander aufgebaut sind.

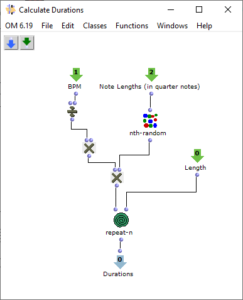
Distanzen berechnen

 

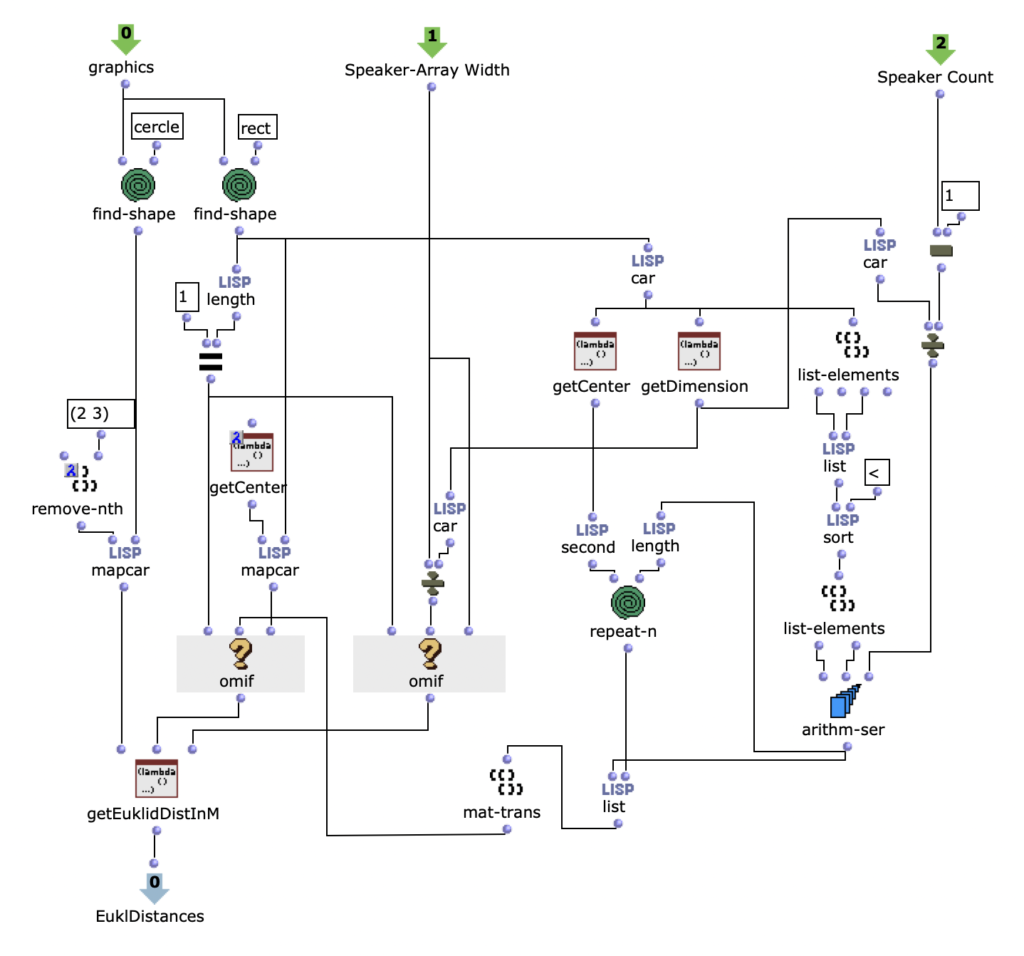
Nach dem Auslesen aller Grafiken des Picture-Objekts müssen diese für die Weiterverarbeitung in Rechteck und Kreise aufgeteilt werden. Falls nur ein Rechteck gefunden wird, kann mit der Position und Dimension des Rechtecks und der beiden Angaben zu Länge und Anzahl des Loudspeaker-Arrays, zunächst die Position jedes einzelnen Loudspeakers innerhalb des Arrays in Metern ermittelt werden. Wenn es mehrere Rechtecke sind, ist dieser Schritt nicht nötig und es werden einfach die Mittelpunkte aller angegebenen Rechtecke ermittelt. Daraufhin ist es möglich im selben Maßstab mit einer weiteren Lisp-Funktion den euklidischen Abstand von allen Quellen zu jedem einzelnen Loudspeaker zu berechnen. Hierbei ist zu beachten, dass alle Grafiken, die in dem Picture-Objekt vom Anwender gezeichnet wurden und nicht einem Rechteck oder einem Kreis entsprechen ignoriert und für die weiteren Berechnungen nicht berücksichtigt werden. Da für die Applikation beliebig viele virtuelle Klangquellen angegeben werden können, werden in diesem Schritt auch alle Kreise erfasst, die im Picture-Objekt existieren, wobei die Reihenfolge irrelevant ist.

Klangverarbeitung

 

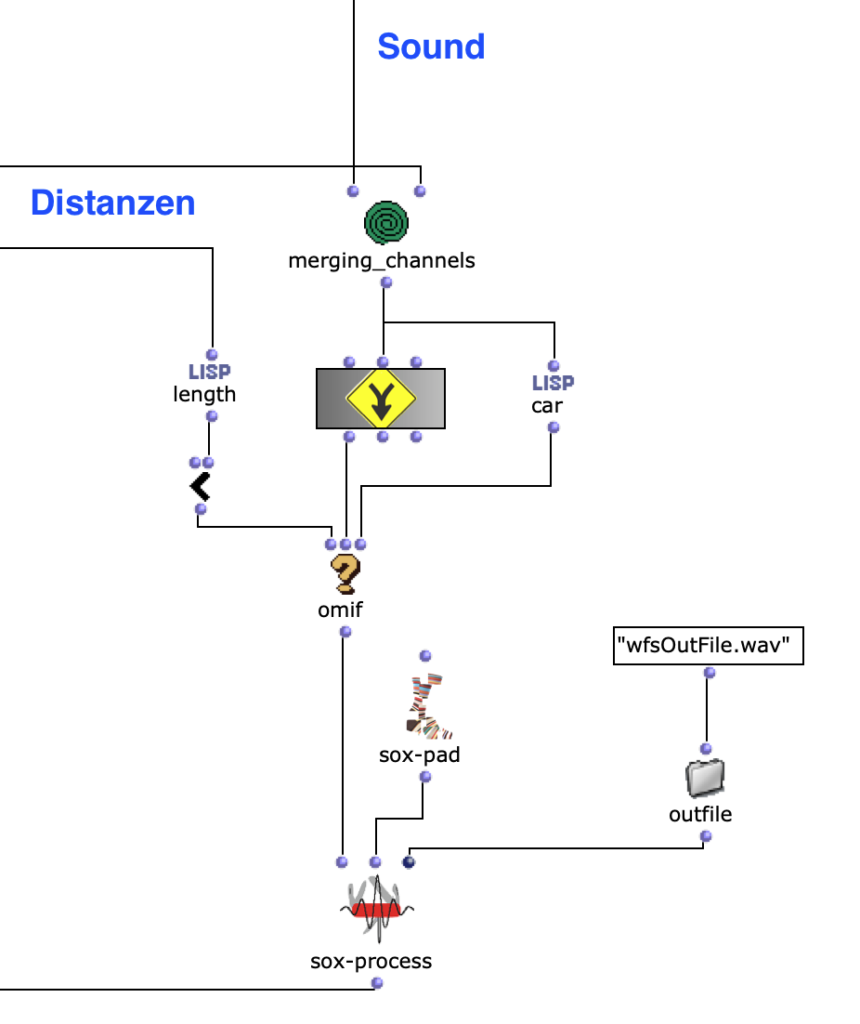
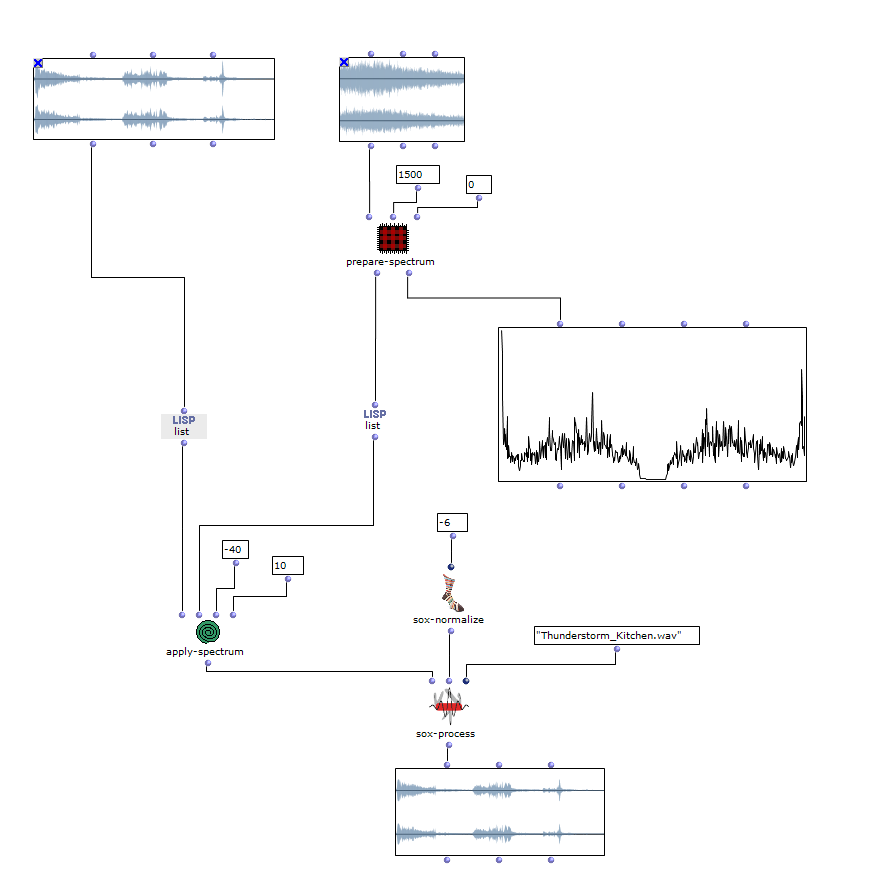
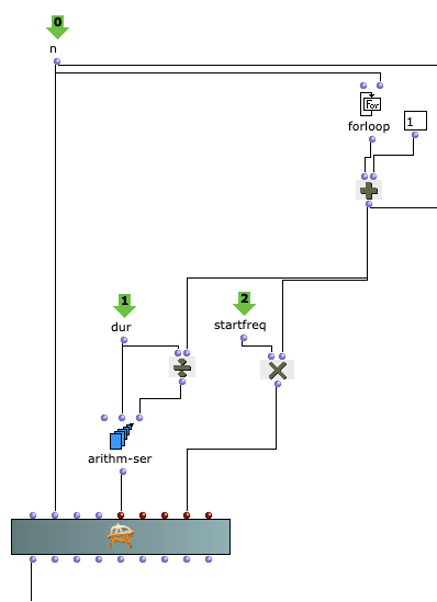
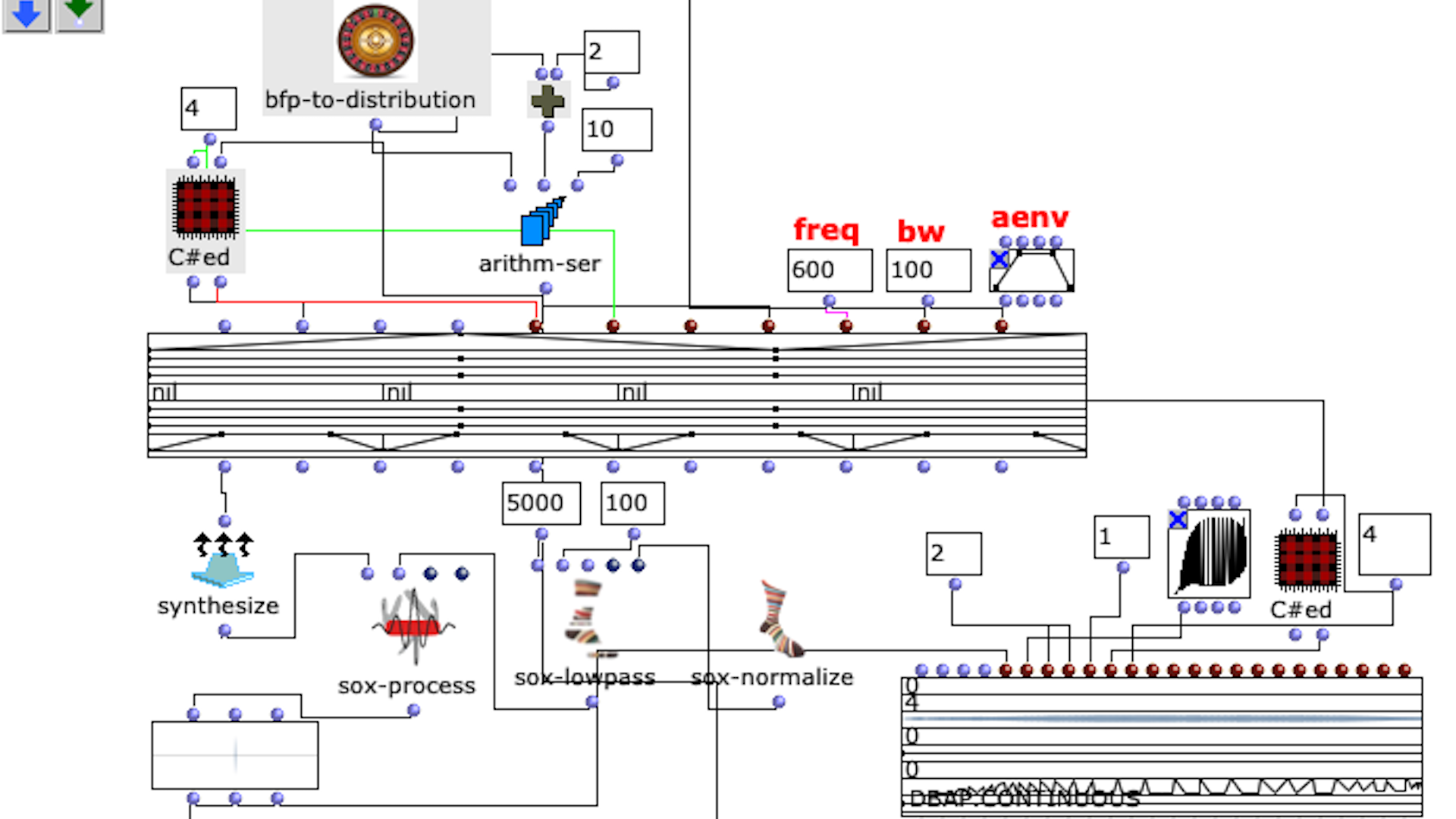
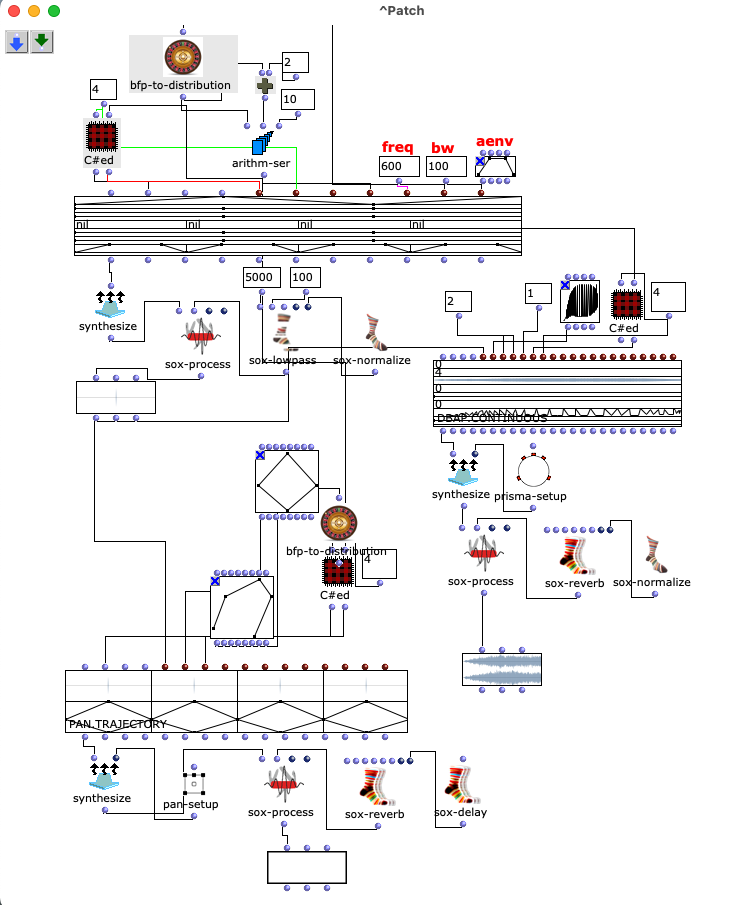
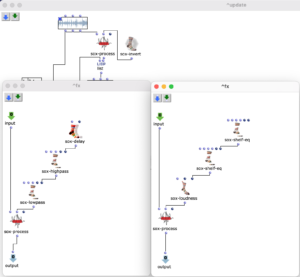
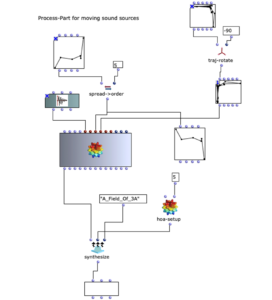
Im nächsten Abschnitt des Programms wird die Klangverarbeitung umgesetzt. Dabei wird grundlegend mit der vom Anwender angegebenen Sound-Datei zusammen mit den zuvor berechneten Distanzen eine Mehrkanaldatei erzeugt, welche für das vorgesehene Loudspeaker-Array verwendet werden kann. Dieser Prozess passiert in einem verschachtelten OM-Loop mit zwei Ebenen.

 

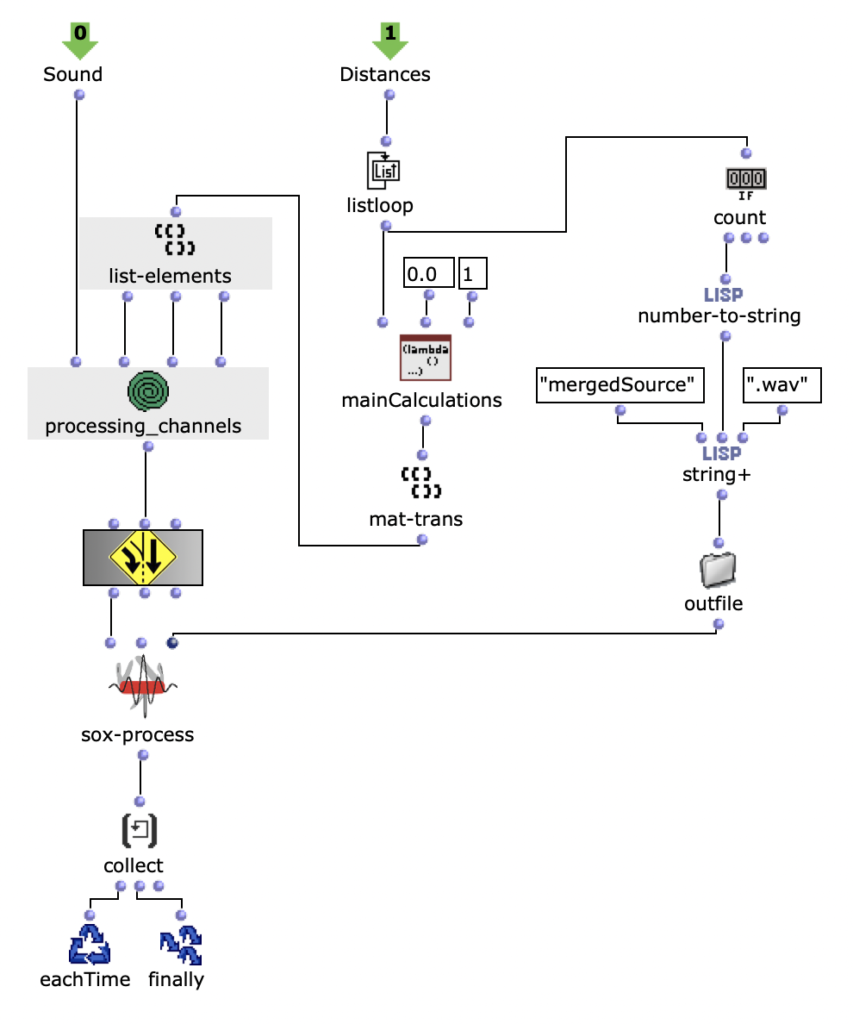
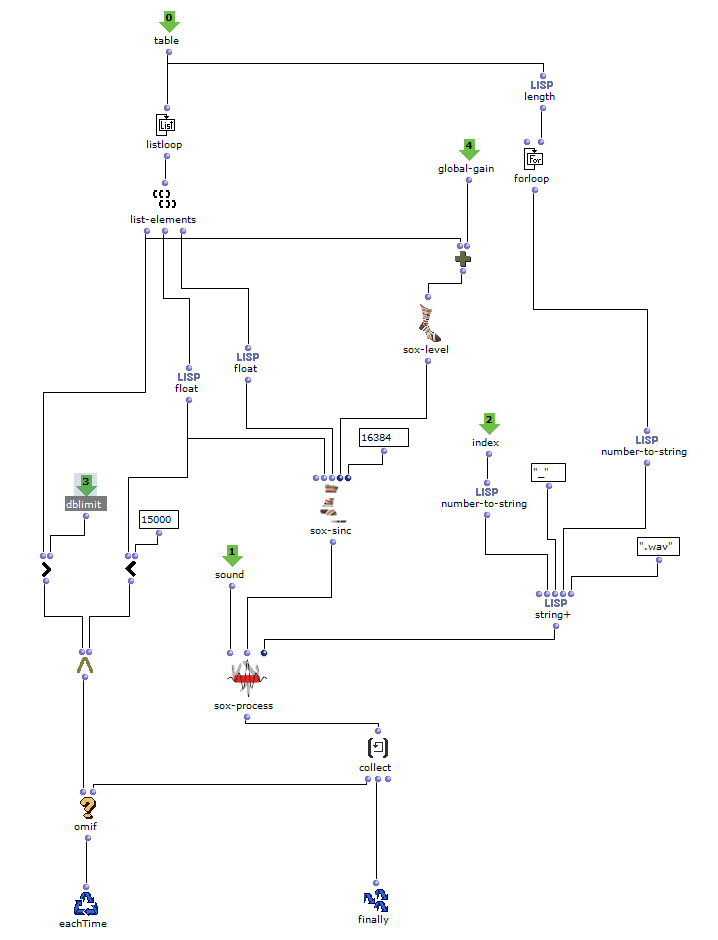
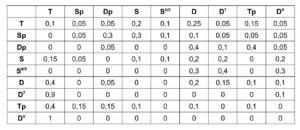
In der ersten Ebene wird zunächst über jedes Element innerhalb der Distanz-Liste iteriert. Dabei entspricht jedes dieser Elemente einer Liste, die zu einer virtuellen Klangquelle gehört, welche deren Distanzen zu jedem Loudspeaker beinhaltet. Bevor der Prozess in die zweite Ebene des Loops geht, werden in einer Lisp-Funktion weitere Berechnungen anhand der aktuellen Distanz-Liste angestellt.

In dieser Funktion wird über jede Distanz iteriert und jeweils die Zeitverzögerung, Lautstärkeabnahme und eine Cutoff-Frequenz für einen Lowpass Filter zur Berechnung der Luftabsorption hoher Frequenzen ermittelt und in einer Liste gesammelt. Mit dem Ergebnis dieser Lisp-Funktion geht es im nächsten Schritt in die zweite Ebene der Schleife.

 

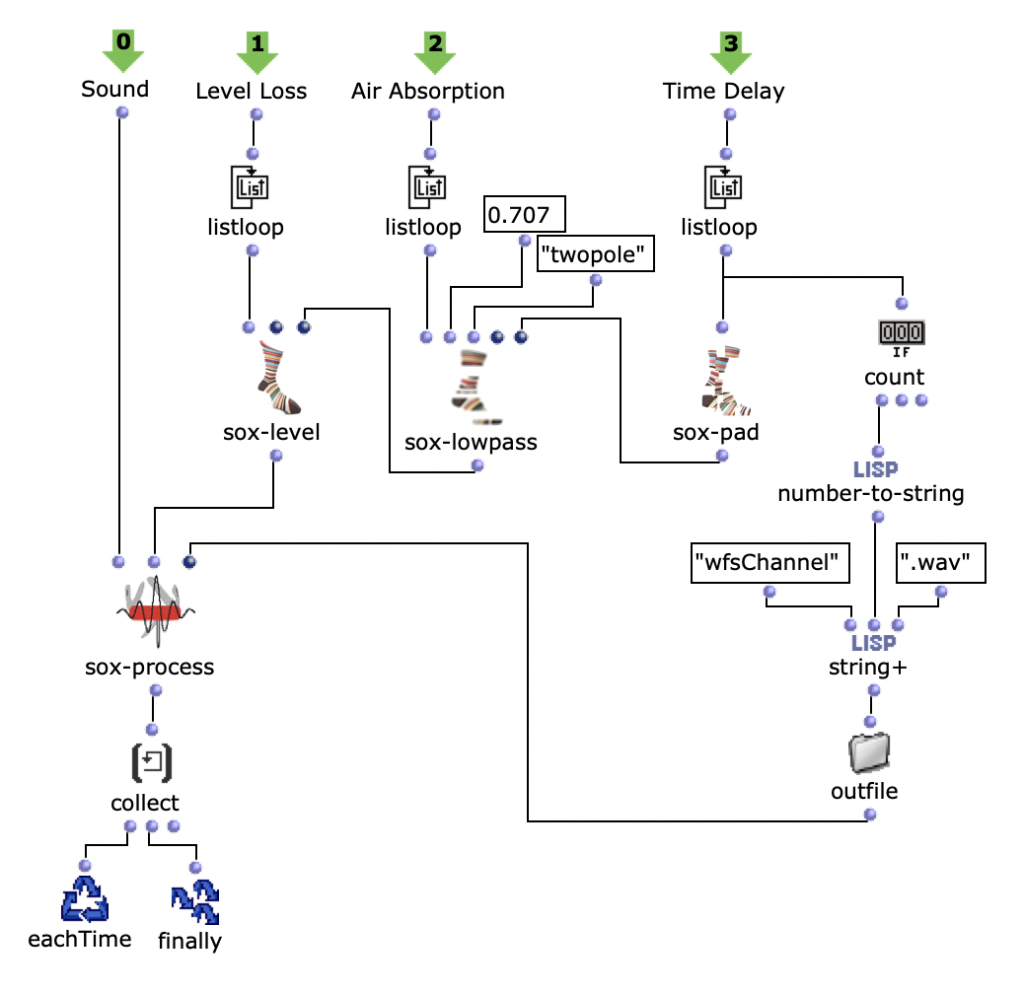
Hier wird für den jeweiligen berechneten Wert den jeweiligen SoX-Effect angewendet; SoX-Level für Lautstärkeabnahme, SoX-Lowpass für die Luftabsorption und SoX-Pad für die Zeitverzögerung. Dabei wird für jede Iteration die entstandene Audiodatei abgespeichert. Jede der drei Listen besitzt so viele Werte, wie zuvor berechnete Distanzen der aktuellen Klangquelle zu den Speakern. Also steht jede in diesem Loop gespeicherte Audiodatei für einen Kanal der späteren Mehrkanaldatei für die aktuellen Klangquelle.

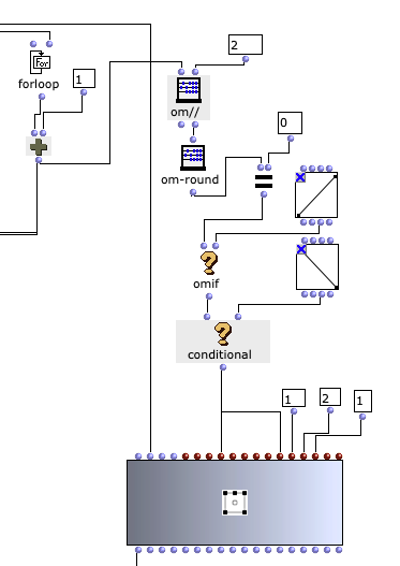
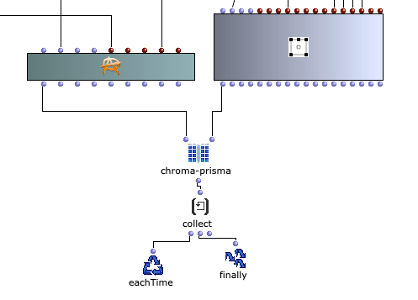
Die Mehrkanaldatei kann nun im nächsten Schritt in der ersten Ebene mit SoX-Merge erstellt und am Ende des Loops zwischengespeichert werden. Dieser Prozess wiederholt sich für alle restlichen virtuellen Klangquellen (sofern vorhanden) und werden als Ausgabe dieses oberen Loops gesammelt. Alle Mehrkanaldateien der jeweiligen Klangquellen werden daraufhin mit einem SoX-Mix zusammengeführt.

Wenn vom Anwender nur eine virtuelle Klangquelle angegeben wird, besteht die Ausgabe des äußersten Loops nur aus einer einzelnen Mehrkanaldatei für diese eine Quelle. In diesem Fall wird das SoX-Mix nicht benötigt und es würde sogar bei der Evaluation des Programms zu einem Fehler führen, wenn der Input des SoX-Mix nur aus einer Audiodatei bestünde. Mit dem OM-If wird daher die Verwendung des SoX-Mix umgangen, sobald die Ausgabe des Patchers, in welchem die Distanzen ermittelt werden, nur aus einer Liste besteht, was bedeutet, dass im Picture-Objekt nur ein Kreis für eine virtuelle Klangquelle gezeichnet wurde.

Abschließend kann mit dem SoX-Pad je nach Präferenz zusätzlich der Mehrkanaldatei Stille hinzugefügt werden, falls die gewählte Audiodatei beispielsweise besonders kurz ist. Gleichzeitig wird die finale Mehrkanaldatei in Outfile als „wfsOutFile.wav“ gespeichert.

VonFlorian Simon
,

Interspaces – Akusmatische Studie mit OM-SoX

Interspaces („Zwischenräume“) stellt Klänge der menschlichen Zivilisation solchen aus der Natur gegenüber. Es werden vier Paare aus Feldaufnahmen vorgestellt, die nach dem Prinzip eines Vocoders gemäß des Spektrums eines Ausschnittes des Gegenstücks gefiltert werden.

Verantwortliche: Florian Simon

Interspaces zeigt folgende vier Paare (Format: Gesamtaufnahme – Quelle des Spektrums):

  1. Zwitschernde Küstenseeschwalben – Von Menschen gerufener Vokal „E“
    Lebendiger Markt, sprechende und rufende Menschen – Ruf der Küstenseeschwalbe

  2. Plätschern eines Flusses – Beschleunigendes Auto
    Hauptverkehrsstraße – Rauschen eines Flusses

  3. Waldkulisse, Blätterrauschen und Vögel – Zughorn
    Bahnhofshalle – Zwitschern eines Singvogels

  4. Gewitter – Klirren von Besteck
    Betrieb in einer Restaurantküche – Donner

Die Feldaufnahmen stammen dabei aus der Bibliothek FreeToUseSounds.

Interspaces nutzt eine gleichseitig oktogonale Lautsprecheranordnung, wobei die beiden Kanäle des Ausgangsmaterials jeweils an gegenüberliegenden Punkten im Array platziert werden. Die zwei Aufnahmen eines Paares sind zudem standardmäßig um 90 Grad zueinander versetzt, sodass vier Klangquellen wahrgenommen werden können.

Jede Aufnahme wird in mehrere Abschnitte von in einem bestimmten Rahmen zufälliger Größe unterteilt und in wiederum randomisierter Reihenfolge mit kurzen Crossfades wieder konkateniert. Die Anzahl der Abschnitte wird mit jedem Aufnahmepaar größer: 4, 9, 16 und zuletzt 23. Mit jedem neuen Abschnitt „wandern“ die beiden Klangquellen zudem im Array um 0,25 Kanäle in eine bestimmte Richtung. Da zwar die Anzahl der Abschnitte für beide Aufnahmen eines Paares dieselbe ist, nicht aber die Position der Schnitte, entstehen Abweichungen von der Basis eines 90-Grad-Abstands sowie eine größere klangliche Vielfalt. Interspaces ist als Installation konzipiert, um eine freie Erkundung der Stereofelder zu ermöglichen.

Interspaces entstand in OpenMusic mithilfe von Funktionen aus der Bibliothek OM-SoX. Das zugrunde liegende Programm besteht aus zwei Teilen. Der erste dient der Herstellung der manipulierten Aufnahmen durch Spektralanalyse (sox-dft), Zerlegung des Ausgangsmaterials in bis zu 4096 Frequenzbänder (sox-sinc), Anpassung deren Lautstärkepegel gemäß des generierten Spektrums (sox-level) und erneutes Zusammensetzen (sox-mix).

Der zweite Programmteil nutzt den Synthesepatch einer Maquette, um für jede der acht generierten Audiodateien die Unterteilung in Abschnitte (sox-trim) sowie deren Spatialisierung (sox-remix) und letztendliche Aneinanderreihung (sox-splice) zu regeln und schlussendlich die fertigen Blöcke zeitlich zu organisieren (sox-pad und sox-mix). Beim letzten Schritt muss die durch die Crossfades eingesparte Zeit berücksichtigt und vom Onset-Wert/x-Position in der Maquette abgezogen werden.

Audio (binaural auf Stereo gemischt):

 

Leider bringt diese Vocoder-Methode den Nachteil mit sich, dass die einzelnen Frequenzbänder zunächst sehr leise sind und deshalb durch das Applizieren des Gains und die finale Normalisierung Artefakte in Form von Rauschen entstehen. Im Gegenzug kommt es zu Clipping, wenn bestimmte Frequenzen gerade in beiden Quellaufnahmen stark vertreten sind. Senkt man die Gain-Werte entsprechend um dies zu vermeiden sind leisere Abschnitte im Resultat je nach Größe der Dynamikdifferenz womöglich kaum mehr hörbar. Das Rauschen lässt sich durch die Wahl höherer Gain-Werte leicht beseitigen, verstärkt damit aber das Clipping-Problem. Bei obiger Version von Interspaces wurde für alle acht Audioclips jeweils der beste Kompromiss zwischen beiden Effekten gesucht.

 

VonAlexander Vozian
, ,

Co-Creative Melody Generator: Visual Live-Coding with OM and Supercollider

Abstract: Der Co-Creative Melody Generator ist ein System für zeitgleiches Live-Coding mit SuperCollider und OpenMusic. Während in OpenMusic die Musik auf Notenebene gestaltet wird, ist SuperCollider für die Klangerzeugung zuständig. Die Kommunikation läuft durch Austausch von Nachrichten im Open-Sound-Control Protokoll per Abfrage durch User oder automatisiert.

Verantwortliche: Alexander Vozian

Überblick:

Die Zielsetzung für das Projekt war Integration von OpenMusic (OM) in einen Live Coding Workflow. Meine erste Idee dazu war es, SuperCollider (SC) für die Klangerzeugung zu verwenden und das Setzen der Noten auf OM auszulagern. Das heißt, man kann in SC live coden und OM als Hilfstool benutzen. In der Erarbeitung wurde aber klar, dass der OM-Patch während der Soundausgabe parallel verändert werden kann. Solange das Klang erzeugende Element nicht unterbrochen wird, kann Live Coding auch in OM stattfinden. Beispielsweise ist es möglich, die Auswahl an “Instrumenten”, in dem Fall SC Synths, vorzubereiten und diese komplett in OM zu steuern. Ein anderer kooperativerer Ansatz wäre, die zwei Programme, SC und OM, auf zwei Live Codende aufzuteilen. Zum Beispiel könnte eine Person in SC die Klanggestaltung übernehmen, während eine andere in OM diese Klänge in Zeit setzt. 

OM kümmert sich um die Generierung der Noten und SC um die Klangsynthese. Diese kommunizieren über das Open Sound Control  (OSC) Protokoll. Der User (Live Codende) schickt in SC eine Anfrage per OSC-Message an den OM-Patch. Die Message enthält Parameter für die Generierung einer Melodie, in dem Fall für eine Markov Analyse und Synthese. Die Message besteht aus:

  • der maximalen Anzahl von Noten,
  • die maximale Länge eines Loops in ms,
  • die Unter- und Obergrenze des zu analysierenden Ausgangsmaterials in ms
  • Auswahl des Ausgangsmaterials.

Das Ausgangsmaterial sind etwa 1 min lange Midi Dateien.

Quellen der Midi Dateien: bitmidi.com

Nach der Synthese schickt OM automatisch eine Message mit der Anzahl der generierten Noten, der Länge der Melodie in ms, einer Liste von Frequenzen und einer Liste von Onsets. Diese werden genutzt, um die Synths in SC zu steuern.

Bei jeder Evaluierung wird Notenmaterial analysiert und eine Liste von Frequenzen und Onsets synthetisiert und dann ausgegeben.

Für die Generierung der Noten werden etwa 1 min lange Midi-Dateien verwendet. Die Pitches und die Durations der Noten werden unabhängig voneinander mit Markov Funktionen erster Ordnung der OM-Alea Bibliothek analysiert, synthetisiert und per osc-send abgeschickt. Dadurch entstehen Tonfolgen, die in den Originaldateien nicht vorkommen. (Im Patch wird sichergestellt, dass die Liste der Pitches und die der Durations gleich lang ist.) Die Eingabeargumente sind bereits oben beschrieben.

Eine OSC-Message von OM zu SC besteht aus folgenden Daten:

  • OSC Key als Identifikator,
  • Gesamtzahl der Noten,
  • Länge der Melodie in Millisekunden,
  • Liste der Frequenzen,
  • Liste der Onsets.

Die Gesamtzahl der Noten wird in dem Fall nur für die Navigation durch die unformatierte OSC Message. Die Länge der Melodie wird benötigt, um den Zeitpunkt zu bestimmen, zu welchem die nächste Melodie angefragt wird. Die Liste der Frequenzen und die der Onsets wird erst in SC zusammengesetzt.

Die osc-send Funktion ist dabei in dem Patch markov_firstorder_osc_send. Um den Patch automatisch auszuführen, wenn eine OSC-Message ankommt, sind alle Teile des übergeordneten Patches auf reactive mode gestellt. Die list Funktion kann erst evaluiert werden, wenn alle Formen ein Ergebnis liefern, das heißt, wenn die Markov-Synthese abgeschlossen und osc-send ausgeführt wurde.

Das Ergebnis ist eine Art Server, der beim Eingang einer Anfrage aus SC automatisch eine Melodie zurückschickt.

In SC wird eine neue Instanz von OSCdef erzeugt, die die erhaltenen Parameter in globale Variablen speichert. Ein Synth(\t1) wird definiert, der von Patterns gespielt werden kann. Die Pfuncn Funktion interpretiert die globalen Variablen ~freq und ~dur als Funktionen und fragt diese damit ständig neu ab. Die Pseq Funktion setzt diese in eine Sequenz um, die von Pbind in als Pattern umgesetzt wird. Somit bildet der erste Parameter von ~freq mit dem ersten Parameter von ~dur die erste Note der Melodie. Die Pdef Funktion erstellt eine Instanz, die während der Laufzeit verändert werden kann. Damit wird auch sicher gestellt, dass ein laufender Loop erst nach Ende einer Melodie eine neue spielt.

Um eine neue Melodie, einen neuen Loop, anzufragen, reicht es, eine OSC-Message mit den entsprechenden Parametern zu schicken. Um diesen Prozess zu automatisieren, benötigt man ein die Funktion Tdef. 

Genauso wie das Ausführen eines Codeblocks in SC direkt Einfluss auf den Klang nehmen kann und somit richtig eingebettet werden muss, muss die Evaluierung eines Patches zur richtigen Zeit erfolgen. Im Falle des MWE wäre nicht der Klang unterbrochen, sondern das Metrum. 

Tdef(\om) berechnet zuerst die Zeitdauer, mit der das Senden der OSC-Message verzögert wird. Die Wartezeit ist abhängig von der Gesamtlänge des Loops und der Anzahl der Loops, welche man innerhalb des Tdef setzen kann. Dabei wird sichergestellt, dass der vorhandene Loop immer zu Ende gespielt wird, bevor die Parameter für einen neue Melodie ankommen.

Der Code zu OM und SC findet sich über diesen Link.

Abschließend noch folgendes Klangbeispiel zum Projekt:

Es wird ausschließlich die maximale Länge eines Loops und die Tonanzahl verändert. Das Ausgangsmaterial wird an zwei Stellen ausgewechselt. Es fängt an mit „Mario“, wechselt bei etwa 1:39 zu „Pokemon“ und bei 2:24 zu „Tetris“. Im Beispiel wird bewusst nichts am Klang des Instruments verändert (einfache Saw-Wave), um einen Fokus auf die Wechsel des Notenmaterials zu setzen.

Mario – Main Theme Overworld:

Pokemon – Battle (vs Wild Pokémon):

Tetris Theme:

Ergebnis:

Quellen der Midi Dateien: bitmidi.com

VonFlorian Simon
, , ,

PixelWaltz: Sonifikation von Bildern in OpenMusic

Abstract: Mit dem OpenMusic-Programm PixelWaltz lassen sich Bilder in symbolische Repräsentation von Musik (Tonhöhen und Einsatzzeitpunkte) umsetzen. Es stehen Optionen zur Bildmanipulation zur Verfügung, mit denen das Resultat zusätzlich beeinflusst werden kann.

Verantwortliche: Florian Simon

Mapping: Pitch

Die Pixel des Bildes werden zeilenweise durchlaufen und die jeweiligen Rot-, Grün- und Blauwerte (zwischen 0 und 1) auf einen gewünschten Tonhöhenbereich gemappt. Aus einem Pixel werden damit stets drei Tonhöhenwerte in Midicent gewonnen. Da zwei nebeneinander liegende Pixel einander in vielen Fällen ähnlich sind, treten bei dieser Mapping-Methode oft sich alle drei Noten wiederholende Muster auf. Hierin liegt der Grund für den Titel des Projektes.

Es besteht auch die Möglichkeit die Anzahl der ausgegebenen Notenwerte zu begrenzen.

Mapping: Einsatzzeitpunkte

Für die Einsatzzeitpunkte und Tondauern kann ein konstanter Wert festgelegt werden. Zudem lässt sich ein Humanizer-Effekt zuschalten, der jede Note innerhalb eines angegebenen Bereiches zufällig nach vorne oder hinten verschiebt. Ausgehend vom Grundtempo lassen sich accelerandi und ritardandi gestalten, indem Listen aus drei Zahlen übergeben werden. Diese stehen für Startnote, Endnote sowie Geschwindigkeit der Tempoänderung. (20 50 -1) sorgt von Note 20 bis Note 50 für ein accelerando, bei dem die Abstände pro Ton um eine Millisekunde kürzer werden. Ein positiver dritter Wert entspricht einem ritardando.

Dynamik

Für die Lautstärke bzw. Velocity lassen sich verschiedene Zufallsbereiche für „rote“, „grüne“ und „blaue“ Noten festlegen. Die so erzeugten Werte können zudem sinusförmig moduliert werden, sodass beispielsweise ein An- und Abschwellen der Lautstärke über längere Zeiträume hinweg möglich ist. Dafür ist die Angabe einer Wellenlänge in Notenzahl sowie des maximalen Abweichungsfaktors nötig.

Begleitstimme

Optional bietet PixelWaltz die Möglichkeit eine Begleitstimme zu generieren, welche aus einzelnen zusätzlichen Tönen in einer gewünschten festen Notenzahlfrequenz besteht. Ist diese nicht durch 3 teilbar, entsteht oft eine Polymetrik. Die Tonhöhe wird zufällig bestimmt und kann dabei zwischen 3 und 6 Halbtönen unter der jeweils „begleiteten“ Note liegen.

Bildbearbeitung

Um weitere Variation zu kreieren sind dem Sonifikationsabschnitt von PixelWaltz Werkzeuge zur Manipulation des Eingangsbildes vorangestellt. Neben der Anpassung von Bildgröße, Helligkeit und Kontrast ist auch eine Verschiebung der Farbwerte und damit ein Umfärben des Bildes möglich. Die Änderungen in der musikalischen Übersetzung sind sofort merkbar: Mehr Helligkeit führt zu einer höheren Durchschnittstonhöhe, mehr Kontrast verkleinert die Zahl der verschiedenen Tonhöhenwerte. Bei einem blaudominierten Bild werden die jeweils letzten Noten der Tripel meist die höchsten sein.

Klangergebnisse

Die klanglichen Resultate unterscheiden sich natürlich je nach Input – gerade fotografiertes Material führt aber oft zu derselben wellenartigen Gesamtstruktur, die sich unregelmäßig und in langsamem Tempo chromatisch mal aufwärts, mal abwärts windet. Die Begleitung unterstützt diesen Effekt und kann einen Gegenpuls zur Hauptstimme bilden.

VonLaura Peter
, , ,

Whitney Music Box mit OMChroma/OMPrisma in OpenMusic

Die Whitney Music Box ist eine sonifizierte und/oder visuelle Darstellung einer Reihe zusammenhängender Sound-Elemente. Diese Elemente können musikalisch gesehen beispielsweise chromatisch oder harmonisch zusammenhängen. In der visuellen Darstellung wird jedes dieser Elemente mit einem Kreis oder Punkt dargestellt (siehe Abbildung 1). Diese Punkte kreisen je nach eigener zugewiesener Frequenz um einen gemeinsamen Mittelpunkt. Je kleiner die Frequenz, desto kleiner der Radius des Umlaufkreises und desto höher die Umlaufgeschwindigkeit. Jedes Sound-Element repräsentiert in einer harmonischen Reihe Vielfache einer festgelegten Grundfrequenz. Sobald ein Element einen Umlauf um den Mittelpunkt vollbracht hat wird der Sound mit der zu repräsentierenden Frequenz ausgelöst. Durch die mathematische Beziehung zwischen den einzelnen Elementen gibt es Momente während der Ausführung der Whitney Music Box in denen bestimmte Elemente gleichzeitig ausgelöst werden und Phasen, in denen die Elemente konsekutiv wahrgenommen werden können. Zu Anfang und am Ende werden alle Elemente gleichzeitig ausgelöst.

Abbildung 1: Whitney Music Box – visuelle Darstellung

Im Rahmen dieses Projekts wird OMChroma für die Synthese der einzelnen Soundelemente verwendet (siehe Abbildung 2). Die Synthese-Klassen von OMChroma erben von OpenMusic’s class-array Objekt. Die Spalten in dem Array beschreiben die einzelnen Komponenten innerhalb der Synthese. Die Reihen repräsentieren Parameter, die den einzelnen Komponenten lokal oder dem gesamten Prozess global zugewiesen können. Für die Whitney Music Box werden Elemente gebraucht, die die einzelnen Tonhöhenabstufungen und die zeitliche Versetzung der einzelnen Tonhöhenabstufungen umsetzt. Dabei wird eine OMChroma-Matrix als Event angesehen. Ein solches Event repräsentiert eine Tonhöhe und die Sound-Wiederholungen innerhalb der globalen Dauer der Whitney Music Box. Die globale Dauer wird zu Anfang festgelegt und beschreibt zugleich die Umlaufzeit der niedrigsten Frequenz bzw. der zuvor festgelegten Startfrequenz. Jede Matrix repräsentiert eine Frequenz, die ein Vielfaches der Startfrequenz ist. Die Umlaufzeit eines Soundelements ergibt sich durch die Formel:

duration(global) / n

Dabei ist n der Index der einzelnen Soundelemente bzw. Matrizen. Je höher der Index, desto höher ist auch die Frequenz und desto kleiner die Umlaufzeit. Die Wiederholungen der Sound-Elemente, wird durch den Parameter e-dels festgelegt. Jede Komponente einer Matrix erhält ein unterschiedliches Entry-Delay. Diese Entry-Delays stehen in einem regelmäßigen Abstand von duration(global) / n zueinander.

 

Abbildung 2: Anwendung von OMChroma

Ohne Spatialisierung hört sich die Whitney Music Box mit OMChroma wie folgt an:

In Abbildung 3 wird dargestellt, wie die gesammelten Matrizen oder Sound-Events mit der Bibliothek OMPrisma spatialisiert werden. Dabei wurde sich an der visuellen Darstellung der Whitney Music Box orientiert. Dabei sind Sound-Elemente mit niedriger Frequenz weiter vom Mittelpunkt entfernt und Soundelemente mit hoher Frequenz kreisen umso näher um den Mittelpunkt. Mit OMPrisma soll diese Darstellung im Raumklang umgesetzt werden. Das heißt, Sounds mit niedriger Frequenz sollen sich weiter entfernt anhören und Sounds mit hoher Frequenz nah am Hörer. Im OpenMusic-Patch wurden zusätzlich Elemente mit geradem Index weiter nach vorne & weiter nach rechts positioniert und analog Elemente mit ungeradem Index weiter nach links und nach hinten positioniert, um die Sounds gleichmäßig im Raum zu verteilen. Die Klassen von OMPrisma bieten zudem noch Presets für die attenuation-function, air-absorption-function und time-of-flight-function an. Diese wurden eingesetzt, um zusätzlich zu der Positionierung im Raum noch mehr Gefühl von Räumlichkeit zu schaffen.

Abbildung 3: Anwendung von OMPrisma

In Stereo hört sich die Whitney Music Box beispielsweise wie folgt an:

In Abbildung 4 wird dargestellt, wie die gesammelten OMChroma- und OMPrisma-Matrizen über die chroma-prisma-Funktion zusammengelegt. Die Liste aller gesammelten Matrizen werden über einen om-loop zurückgegeben und über die synthesize-Funktion als Sound gerendert (siehe Abbildung 5).

Abbildung 4: chroma-prisma

Abbildung 5: loop und synthesize

Der OpenMusic-Patch sowie Soundbeispiele können unter folgenden Links abgerufen werden:

Projektdateien Stand: 12.10.2023

Github Repository

VonMoritz Reiser
, ,

Markov-Prozesse zur Steuerung von Harmonik in Open Music und Common Lisp

Abstract: Ein Projekt über den Einsatz von Zufallsprozessen in einem musikalischen Kontext. Grundsätzlich kommen zwei verschiedene Modelle zum Einsatz. Diese erzeugen Akkordfolgen, welche anschließend mit einem Rhythmus und einer darüber liegenden Melodie ausgestattet werden.

Verantwortliche: Moritz Reiser

 

Überblick

Der Gesamtaufbau des Programms, welcher dem Inhalt des Hauptpatches entspricht, ist in Abbildung 1 zu sehen. Ganz oben befindet sich die Auswahl des zu verwendenden Algorithmus zur Akkordfolgenerzeugung. Über das Auswahlfeld links oben kann dieser ausgewählt werden. Durch die beiden Inputfelder der Subpatches lassen sich jeweils die gewünschte Länge sowie der Startakkord bzw. die Tonart der Komposition festlegen.

Anschließend folgt eine zufällige Bestimmung der jeweiligen Tonlängen. Hier lassen sich das Tempo in BPM sowie die Häufigkeiten der vorkommenden Tonlängen in Vielfachen von Viertelnoten einstellen. Über eine „dx→x“-Funktion werden aus den berechneten Dauern die jeweiligen Startzeitpunkte der Akkorde berechnet. Hier muss beim Verwenden des Programms darauf geachtet werden, dass Open Music aufgrund des zweimal verwendeten Outputs in den beiden Strängen jeweils neue Zufallszahlen berechnet, wodurch der Bezug zwischen Startzeitpunkt und Tondauer verloren geht. Abhilfe kann hier dadurch geschaffen werden, dass nach einmaliger Ausführung die Subpatches der Akkordfolgen- und der Tonlängengenerierung mit „Lock Eval“ gesperrt werden und das Programm anschließend noch einmal ausgeführt wird, um die Startzeitpunkte an die nun gespeicherten Tondauern anzupassen (siehe Hinweistafel im Hauptpatch). Der dritte große Schritt des Gesamtablaufs besteht schließlich in der Generierung einer Melodie, die über der Akkordfolge liegt. Hier wird jeweils ein Ton aus dem zugrunde liegenden Akkord ausgewählt und eine Oktave nach oben verschoben. Dabei kann eingestellt werden, ob dies immer ein zufälliger Akkordton sein soll, oder ob der Ton gewählt wird, welcher dem vorangehenden Melodieton am nächsten bzw. am weitesten entfernt ist.

Das Resultat wird schließlich ganz unten in einem Multi-Seq-Objekt visualisiert.

Abbildung 1: Gesamtaufbau des Kompositionsprozesses

 

Akkordfolgengenerierung

Zur Generierung der Akkordfolge stehen zwei Algorithmen zur Verfügung. Ihnen wird jeweils die gewünschte Länge der Sequenz, welcher der Anzahl der Akkorde entspricht, und der Startakkord bzw. die Tonart übergeben.

Harmonische Akkordfolge mittels Markovkette

Der Ablauf des ersten Algorithmus ist in Abbildung 2 zu sehen. Durch den Subpatch „Create Harmonic Chords“ wird der Grundvorrat von Akkorden erzeugt, der im Folgenden verwendet wird. Dieser entspricht den üblichen Stufen der Kontrapunktlehre und enthält neben Tonika, Subdominante, Dominante und deren Parallelen einen verminderten Akkord auf der siebten Stufe, einen Sixte ajoutée der Subdominante und einen Dominantseptakkord. Der „Key“-Input addiert zu diesen Akkorden einen der gewünschten Tonart entsprechenden Wert hinzu.

Abbildung 2: Subpatch zur Generierung einer harmonischen Akkordsequenz mithilfe einer Markovkette

Durch den Subpatch „Create Transition Matrix“ wird eine Matrix mit Übergangswahrscheinlichkeiten der einzelnen Akkorde erzeugt. Für jede Akkordstufe wird festgelegt, mit welcher Wahrscheinlichkeit sie zu einem bestimmten anderen Akkord übergeht. Die Wahrscheinlichkeitswerte wurden hierbei willkürlich gemäß den in der Kontrapunktlehre üblichen Abläufen gewählt und experimentell angepasst. Dabei wurde für jeden Akkord untersucht, wie wahrscheinlich aus diesem jeweils in einen anderen Akkord übergegangen wird, sodass das Resultat den Konventionen der Kontrapunklehre entspricht und eine häufige Rückkehr zur Tonikastufe ermöglicht, um diese zu fokussieren. Die exakten Übergangswahrscheinlichkeiten sind in der folgenden Tabelle aufgelistet, wobei die Ausgangsklänge in der linken Spalte aufgelistet sind und die Übergänge jeweils zeilenweise repräsentiert werden.

Tabelle 1. Übergangswahrscheinlichkeiten der Harmonien entsprechender Akkordstufen

Die Erzeugung der Akkordfolge findet schließlich in dem Patch „Generate Markov Series“ statt, welcher in Abbildung 3 dargestellt ist. Dieser arbeitet zunächst nur mit Nummerierungen der Akkordstufen, weshalb es genügt, ihm die Länge des Akkordvorrats zu übergeben. Die Lisp-Funktion „Markov Synthesis“ erzeugt nun mithilfe der Übergangsmatrix eine Akkordfolge der gewünschten Länge. Da bei der so erzeugten Sequenz nicht sichergestellt ist, dass der letzte Akkord der Tonika entspricht, kommt eine weitere Lisp-Funktion zum Einsatz, welche so lange weitere Akkorde generiert, bis die Tonika erreicht ist. Da bisher nur mit Nummerierungen der Stufen gearbeitet wurde, werden abschließend die für die jeweiligen Stufen gültigen Akkorde ausgewählt, um die fertige Akkordfolge zu erhalten.

Abbildung 3: Subpatch zur Erzeugung einer Akkordfolge mittels Markovsynthese

 
Chromatische Akkordfolge mittels Tonnetz

Im Gegensatz zur harmonischen Akkordfolge kommen hier alle 24 Dur- und Mollakkorde der chromatischen Skala zum Einsatz (siehe Abbildung 4). Die Besonderheit dieses Algorithmus liegt in der Wahl der Übergangswahrscheinlichkeiten. Diese basieren auf einem sogenannten Tonnetz, welches in Abbildung 5 dargestellt ist.

Abbildung 4: Subpatch zur Generierung einer Akkordfolge auf Basis der Tonnetz-Darstellung

Abbildung 5: Tonnetz (Bildquelle: <https://jazz-library.com/articles/tonnetz/>)

Innerhalb des Tonnetzes sind einzelne Töne aufgetragen und miteinander verbunden. Auf den horizontalen Linien haben die Töne jeweils den Abstand einer Quinte, auf den diagonalen Linien sind kleine (von links oben nach rechts unten) sowie große Terzen (von links unten nach rechts oben) zu sehen. Die sich so ergebenden Dreiecke repräsentieren jeweils einen Dreiklang, beispielsweise ergibt das Dreieck der Töne C, E und G den Akkord C-Dur. Insgesamt sind so alle Dur- und Moll-Akkorde der chromatischen Skala zu finden. Zum Einsatz kommt die Tonnetz-Darstellung meist zu Analyse-Zwecken, da sich aus einem Tonnetz direkt ablesen lässt, wie viele Töne sich zwei verschiedene Dreiklänge teilen. Ein Beispiel ist die Analyse von klassischer Musik der Romantik und Moderne sowie von Filmmusik, da hier die oben verwendeten harmonischen Kontrapunktregeln häufig zu Gunsten von chromatischen und anderen zuvor unüblichen Übergängen vernachlässigt werden. Der Abstand zweier Akkorde im Tonnetz kann hierbei ein Maß dafür sein, ob der Übergang des einen Akkords in den anderen wohlklingend oder eher ungewöhnlich ist. Er berechnet sich aus der Anzahl von Kanten, die überquert werden müssen, um von einem Akkord-Dreieck zu einem anderen zu gelangen. Anders ausgedrückt entspricht er dem Grad der Nachbarschaft zweier Dreiecke, wobei sich eine direkte Nachbarschaft durch das Teilen einer Kante ergibt. Abbildung 6 zeigt hierzu ein Beispiel: Um ausgehend vom Akkord C-Dur zum Akkord f-Moll zu gelangen, müssen drei Kanten überquert werden, wodurch sich ein Abstand von 3 ergibt.

Abbildung 6: Beispiel der Abstandsbestimmung im Tonnetz anhand des Übergangs von C-Dur nach f-Moll

Im Rahmen des Projekts werden nun die Übergangswahrscheinlichkeiten auf Basis der Abstände von Akkorden im Tonnetz berechnet. Hierbei muss lediglich unterschieden werden, ob es sich bei dem jeweils aktiven Dreiklang um einen Dur- oder Mollakkord handelt, da sich innerhalb dieser beiden Klassen für alle Tonarten dieselben Abstände zu anderen Akkorden ergeben. Dadurch kann jeder Übergang von C-Dur bzw. c-Moll aus berechnet und anschließend durch Addition eines Wertes in die gewünschte Tonart verschoben werden. Von beiden Varianten (C-Dur und c-Moll) ausgehend wurden zunächst die Abstände zu allen anderen Dreiklängen im Tonnetz festgehalten:

Abstände von C-Dur:

Abstände von c-Moll:

Um aus den Abständen Wahrscheinlichkeiten zu erhalten wurden zunächst alle Werte von 6 abgezogen, um größere Abstände unwahrscheinlicher zu machen. Anschließend wurden die Resultate als Exponent der Zahl 2 verwendet, um nähere Akkorde stärker zu gewichten. Insgesamt ergibt sich somit die Formel

P=2^(6-x) ; P=Wahrscheinlichkeit,  x=Abstand im Tonnetz

zur Berechnung der Übergangsgewichtungen. Diese ergeben sich für alle möglichen Akkordkombinationen zu folgender Matrix, aus welcher bei Division durch die Zeilensumme 342 Wahrscheinlichkeiten resultieren.

Innerhalb des Patches stellt die Lisp-Funktion „Generate Tonnetz Series“ zunächst jeweils fest, ob es sich bei dem aktiven Akkord um einen Dur- oder Molldreiklang handelt. Da wie bei der harmonischen Vorgehensweise zunächst nur mit den Zahlen 0-23 gearbeitet wird, kann dies über eine einfache Modulo-2-Rechnung bestimmt werden. Je nach Resultat wird der jeweilige Wahrscheinlichkeiten-Vektor herangezogen, ein neuer Akkord bestimmt und schließlich die vorherige Stufe hinzuaddiert. Ergibt sich eine Zahl, die größer als 23 ist, wird 24 abgezogen, um immer innerhalb der selben Oktave zu bleiben.

Nach der zuvor festgelegten Länge der Sequenz ist dieser Abschnitt beendet. Auf eine Rückführung zur Tonika wie im vorherigen Abschnitt wird hier verzichtet, da aufgrund der Chromatik keine so stark ausgeprägte Tonika vorherrscht wie bei der harmonischen Akkordfolge.

Bestimmung der Tonlängen

Nach der Generierung einer Akkordfolge werden für die einzelnen Dreiklänge zufällige Längen berechnet. Dies geschieht im Subpatch „Calculate Durations“, der in Abbildung 6 dargestellt ist. Neben der gewünschten BPM-Zahl wird ein Vorrat an Tonlängen als Vielfache von Viertelnoten übergeben. Wahrscheinlichere Werte kommen in diesem Vorrat häufiger vor, sodass über „nth-random“ eine entsprechende Wahl getroffen werden kann.

Abbildung 7: Subpatch zur zufälligen Bestimmung der Tondauern

Melodiegenerierung

Der grundsätzliche Ablauf der Melodiegenerierung wurde oben bereits dargestellt: Aus dem jeweiligen Akkord wird ein Ton ausgewählt und um eine Oktave nach oben transponiert. Dieser Ton kann zufällig oder entsprechend dem kleinsten oder größten Abstand zum Vorgängerton gewählt werden.

 

Klangbeispiele

Beispiel für eine harmonische Akkordfolge:

 
 

Beispiel für eine Tonnetz-Akkordfolge:

 
 
VonAndres Kaufmes
, , , ,

Räumliche Granularsynthese mit Hilfe von stochastischen Prozessen

Räumliche Granularsynthese mit Hilfe von stochastischen Prozessen

VPRS – Visuelle Programmierung der Raum/Klangsynthese

Prof. Dr. Marlon Schumacher

Abschlussprojekt von Andres Kaufmes 

HfM Karlsruhe – IMWI (Institut für Musikinformatik und Musikwissenschaft)

SoSe 2023

_____________

Für das Abschlussprojekt im Seminar „Visuelle Programmierung der Raum/Klangsynthese“ wurden die Open Music Libraries OMChroma, OMPrisma, Alea und OM-Sox verwendet. OMChroma wurde mit Hilfe der Klasse „FOF-1“ zur Klangsynthese verwendet und OMPrisma zur räumlichen Spatialisierung mit Hilfe der Klassen „Pan“ und „DBAP“. Die Library „Alea“ diente zur zufälligen Steuerung ausgewählter Parameter, mit OM-Sox wurden schließlich Reverb und Delay zum Signal hinzugefügt.

Om-Patch.

Abildung: Open Music Patch

Der Open Music Patch ist wie folgt aufgebaut: Der durch die FOF-1 Klasse synthetisierte Klang wird durch Sox-Lowpass gefiltert und durch Sox-Normalize normalisiert und in eine Soundfile geschrieben. Der Buffer wird nun in die Spatialisierungsklassen (Pan und DBAP) eingespeist, welche dann das nun spatialisierte Signal erneut als Soundfile speichern. Die Parameter des FOF-1 Objekts werden durch ein „BFP-to-Distribution“ Objekt der „Alea“ Library gesteuert, welches die gleiche Hüllkurve wie das FOF-1 Objekt als Input nutzt, um so Parameter für die Klangsynthese zu erstellen. Die ursprüngliche Idee, einen binauralen Renderer zu nutzen ließ sich aufgrund von Kompatiblitäts-Problemen mit der Software leider nicht implementieren, daher wurde mit den „Pan“ und „DBAP“ Objekten gearbeitet. Das Pan Objekt wird ebenfalls durch ein BFP-to-Distribution Objekt der Alea Library gesteuert. Am Ende der Signalkette fügt ein Sox-Process Objekt noch Reverb und Delay zum Audiosignal hinzu.

Klangbeispiel

VonMarlon Schumacher
, , , , ,

Music for Headphones

Vorstellung des Projekts eines Alumni beim Ircam Forum 23 in Paris mit Software von Marlon Schumacher
Projektverantwortliche: Marco Bidin, Fernando Maglia

Im IRCAM-Forum im März 2023 in Paris (special edition zum Thema AR/VR Spatialization) hat der ehemalige Student und Mitarbeiter Marco Bidin Projekte zum Thema binaurale Klangsynthese vorgestellt, welche durch von Prof. Marlon Schumacher entwickelte Software realisiert wurden. Als Synthese-Werkzeuge kamen  unter Anderem CSound, Cycling 74’s Max, OpenMusic mit der Library OMPrisma zum Einsatz, gemastert wurde in der DAW Logic Pro X. Die Klangsynthese verwendet teils subtraktive Ansätze, Waveguides und andere physikalische Modelle.

 

Ausschnitt eines in Csound implementierten Orchesters.

Music for Headphones III ist eine Produktion von ALEA, Associazione Laboratorio Espressioni Artistiche.

Zur Beschreibung der Präsentation geht es mit diesem Link.

Im folgenden Video sind Klangbeispiele zu hören, für welche Teile des Programmcodes und Workflows demonstriert werden.

VonAndres Kaufmes
, , , ,

Transient Processor

Transient Processor

SKAS-Symbolische Klangverarbeitung und Analyse/Synthese

Prof. Dr. Marlon Schumacher

Zwischenprojekt von Andres Kaufmes 

HfM Karlsruhe – IMWI (Institut für Musikinformatik und Musikwissenschaft)

WiSe 2022/23

_____________

 

Für dieses Zwischenprojekt habe ich mich mit der Implementierung eines Transient- Prozessors in OpenMusic mit Hilfe der OM-Sox Library beschäftigt.
Mit einem Transient Prozessor (auch Transient Designer oder Transient Shaper) lässt sich das Ein- und Ausschwingverhalten (Attack/Release) der Transienten eines Audiosignal beeinflussen.

Das erste vorgestellte Hardware Gerät war der 1998 von der Firma SPL vorgestellte SPL TD4, welcher als 19″ Rack-Gerät erhältlich war und in fortgeschrittener Version bis heute erhältlich ist.

           

Transient Designer der Firma SPL.  (c) SPL 

Transient Designer eignen sich besonders für die Bearbeitung von perkussiven Klängen oder auch für Sprache. Zunächst müssen die Transienten aus dem gewünschten Audiosignal isoliert werden, dies lässt sich zum Beispiel mit Hilfe eines Kompressors umsetzen. Durch eine kurze Attack-Zeit werden die Transienten „geduckt“ und das Signal kann vom Original abgezogen werden. Anschließend kann das Audiosignal im Verlauf der Signalkette mit weiteren Effekten bearbeitet werden.

Transient-Prozessor Patch.                        FX- Kette der beiden Signalwege (links „Transient“, rechts „Residual“).

Im Patch zu sehen ist an oberster Stelle die zu bearbeitende Audiodatei, von welcher, wie eben beschrieben, mit Hilfe eines Kompressors die Transienten isoliert, und das resultierende Signal vom originalen abgezogen wird. Nun werden zwei Signalwege gebildet: Die isolierten Transienten werden in der linken „Kette“ verarbeitet, das residuale Signal in der rechten. Nachdem beide Signalwege mit Audioeffekten bearbeitet wurden, werden sie zusammengemischt, wobei das Mischverhältnis (Dry/Wet) beider Signalwege nach belieben eingestellt werden kann. Am Ende der Signalverarbeitung befinden sich ein globaler Reverb-Effekt.

„Scope“ Ansicht der beiden Signalwege.               Skizzen zum möglichen Signalweg und Verarbeitung.

Klangbeispiele:

Isoliertes Signal:

Residuales Signal:

VonJakob Schreiber
, , , ,

Spatiale Transformation des Stückes »Ode An Die Reparatur«

Abstract: Der Eintrag beschreibt die Spatialisierung des Stückes »Ode An Die Reparatur« (2021) und dessen Transformation in eine Higher Order Ambisonics Version. Ein binauraler Mix des fertigen Stückes ermöglicht es, den Arbeitsprozess anhand des Ergebnisses nachzuvollziehen.

Betreuer: Prof. Dr. Marlon Schumacher

Ein Beitrag von: Jakob Schreiber

Stück

Das Stück »Ode An Die Reparatur« (2021) besteht aus vier Sätzen, von denen jeder sich auf einen anderen Aspekt einer fiktiven Maschine bezieht. Interessant an diesem Prozess war es, den Übergang von Maschinenklängen in musikalische Klänge zu untersuchen und über den Verlauf des Stückes zu gestalten.

Produktion

Die Produktions-Ressourcen des Stückes waren einerseits ein UHER-Tonbandgerät, welches einfache Repitch-Veränderungen ermöglicht und durch seine Funktionsweise mit Motoren und Riemen für die Umsetzung dieses an mechanische Maschinen angelehnten Stückes prädestiniert war. Außerdem kam SuperCollider als digitale Klangsynthese- und Verfremdungsumgebung zum Einsatz.

Aufbau

Das Stück besteht aus vier Sätzen.

Erster Satz

Das Tonmaterial des Beginns setzt sich aus verschiedenen Aufnahmen eines Tonbandgerätes zusammen, über welches neben Stille klar hörbare, synthetisierte Motoren-Klänge abgespielt werden.

Zweiter Satz

Die zu manchen Teilen an Vogelgezwitscher erinnernden Klangobjekte treten teils unvermittelt aus steriler Stille in den Vordergrund.

Dritter Satz

Die perforative Charakteristik im inneren eines Zahnradgetriebes transformiert sich im Verlauf des Satzes zu tonal ausgebildeten Resonanzen.

Vierter Satz

Im letzten Satz spielen die Motoren eine monumental anmutende Abschluss-Hymne.

Spatialisierung

Angelehnt an die kompositorische Form des Stückes halten sich die Spatialisierungs-Entwürfe an die Unterteilung in Sätze.

Arbeits-Praxis

Der Arbeitsprozess lässt sich, ähnlich wie der OM-Patch, in verschiedene Bereiche aufteilen. Im Labor-Abschnitt erforschte ich verschiedene Spatialisierungsformen auf ihre Ästhetische Wirkung hin und untersuchte deren Übereinstimmung mit der kompositorischen Form des bereits bestehenden Stückes.

Um verschiedene Trajektorien, oder feste Positionen von Klangobjekten zu ermitteln spielte neben der auditiven Wirkung auch die visuelle Einschätzung der jeweiligen Trajektorien eine wichtige Rolle.

Letztendlich wurden die Paramter der bereits vorausgewählten Trajektorien mit einem Streuungsverlauf ergänzt, fein justiert und schließlich über eine Kette aus Modulen in ein Higher Order Ambisonics Audiofile fünfter Ordnung transformiert.

In Iterativer Weise werden die synthetisierten Mehrkanal-Dateien in REAPER in das Gesamtgefüge eingepflegt und deren Wirkung untersucht, bevor sie mit einem optimierten Set an Parametern und Trajektorien noch einmal den Syntheseprozess durchlaufen.

Näheres zu den einzelnen Sätzen

Zunächst kann hier die binaurale Version des spatialisierten Stückes als ganzes angehört werden. In der Folge werden kurz die Herangehensweisen der einzelnen Teile beschrieben

 

 
Erster Satz

Die lange gezogenen, wie Schichten übereinander liegenden Klanwolken bewegen sich im ersten Teil dem Grundtempo des Satzes entsprechend. Die Trajektorien liegen dabei in der Summe U-förmig um den Hör-Bereich, wobei sie nur die Seiten und Vorderseite abdecken.

Zweiter Satz

Einzelne Klang-Objekte sollen aus sehr verschiedenen Positionen zu hören sein. Nahezu perkussive Klänge aus allen Richtungen des Raumes lassen die Aufmerksamkeit der Hörer*in springen.

Dritter Satz

Das klangliche Material des Teiles ist eine an den Klang von Zahnrädern, oder eines Getriebes angelehnte Klangsynthese. Das Augenmerk hierbei lag in der Immersion in die fiktive Maschine. Aus eben diesem Klangmaterial entstehen durch Resonanzen und andere Veränderungen liegetöne, die sich zu kurzen Motiven aneinander reihen.

Das Spatialisierungskonzept für diesen Teil setzt sich aus beweglichen und teilweise statischen Objekten Zusammen. Die beweglichen erschaffen zu Beginn des Satzes eine Anmutung von Räumlichkeit Immersion. Zum Ende des Satzes kommen zwei verhätnismäßig statische Objekte links und rechts der Stereobasis hinzu, die vor allem die melodie-haften Aspekte des Klanges hervorheben und an ihrer jeweiligen Position lediglich flüchtig auf der vertikalen Achse oszillieren.

Vierter Satz

Die Instrumentierung dieses Teiles des Stückes setzt sich aus drei Simulationen eines Elektromotors zusammen, die jeweils eine Eigene Stimme verfolgen. Um die einzelnen Stimmen noch etwas besser voneinander zu trennen, entschied ich mich dazu, jeden der vier Motoren als einzelnes Klangobjekt zu behandeln. Um den monumentalen Charakter des Schlussteils zu unterstützen, bewegen sich die Objekte dabei nur sehr langsam durch den fiktiven Raum.

 

Your browser doesn't support the HTML5 CANVAS tag.