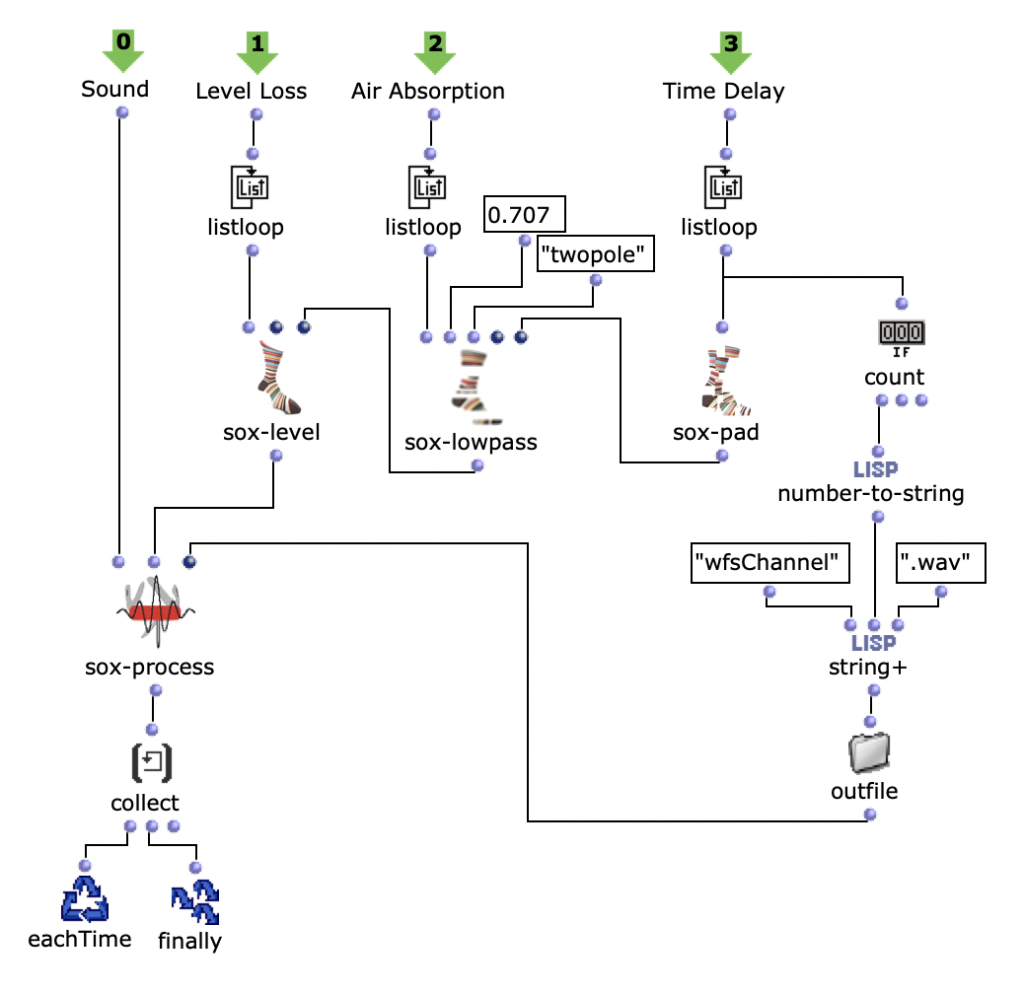
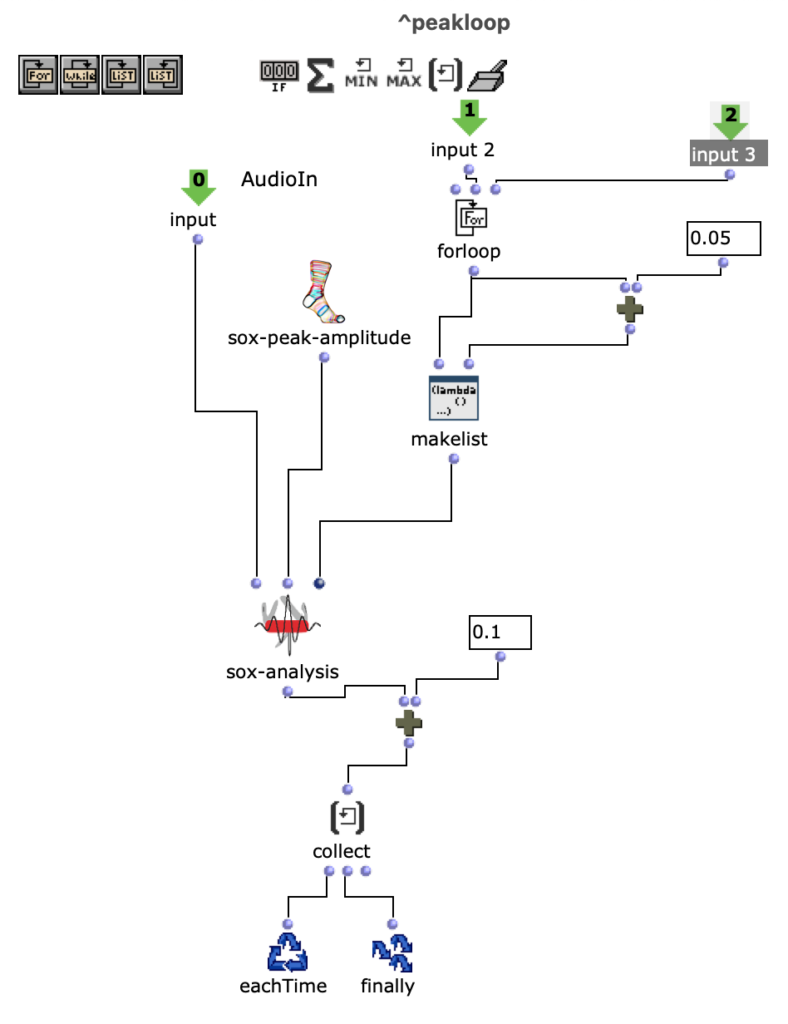
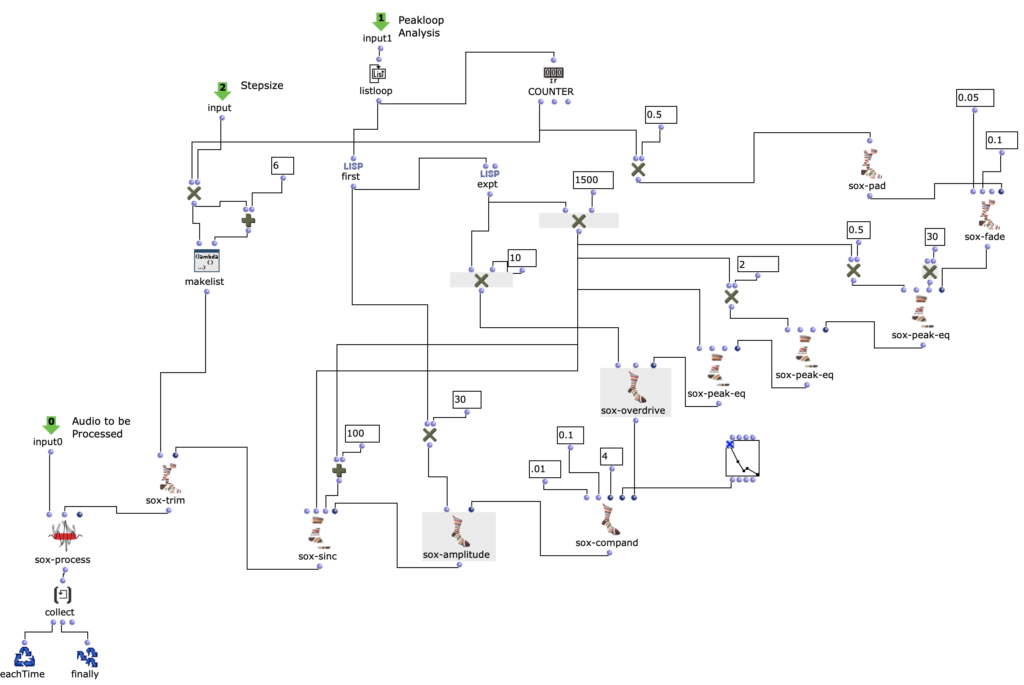
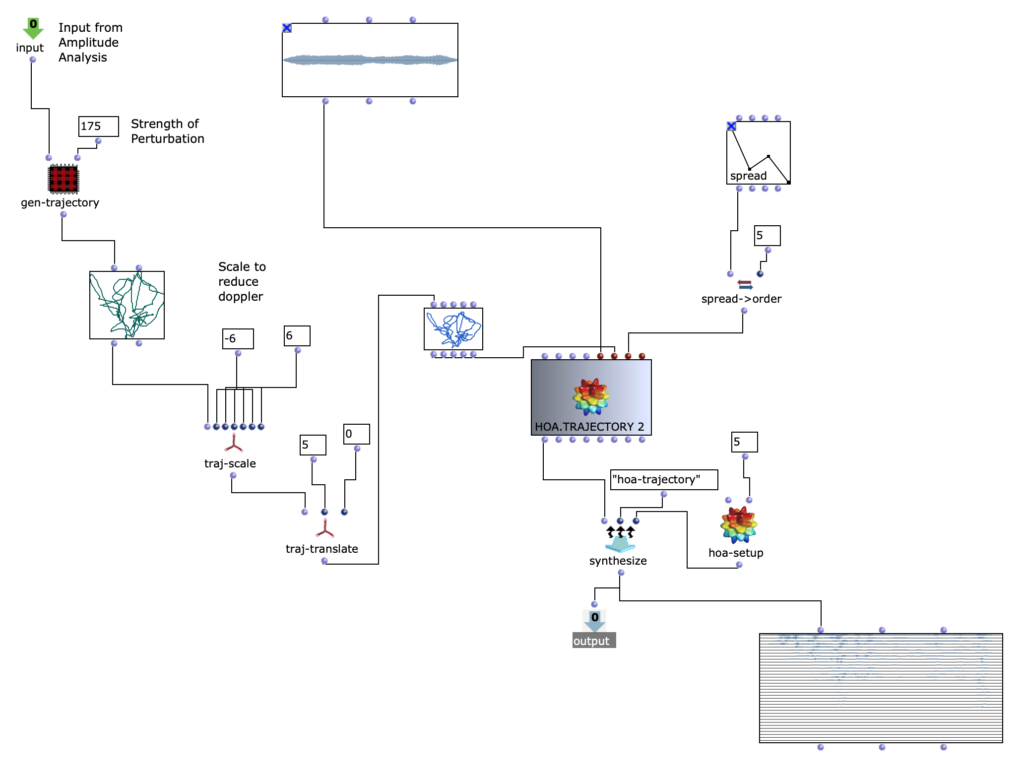
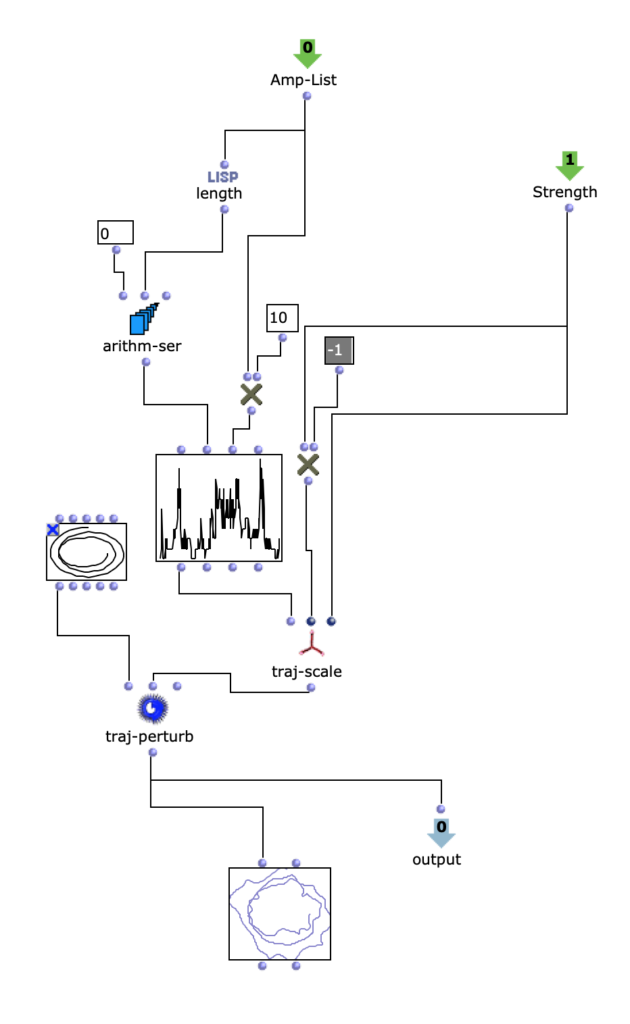
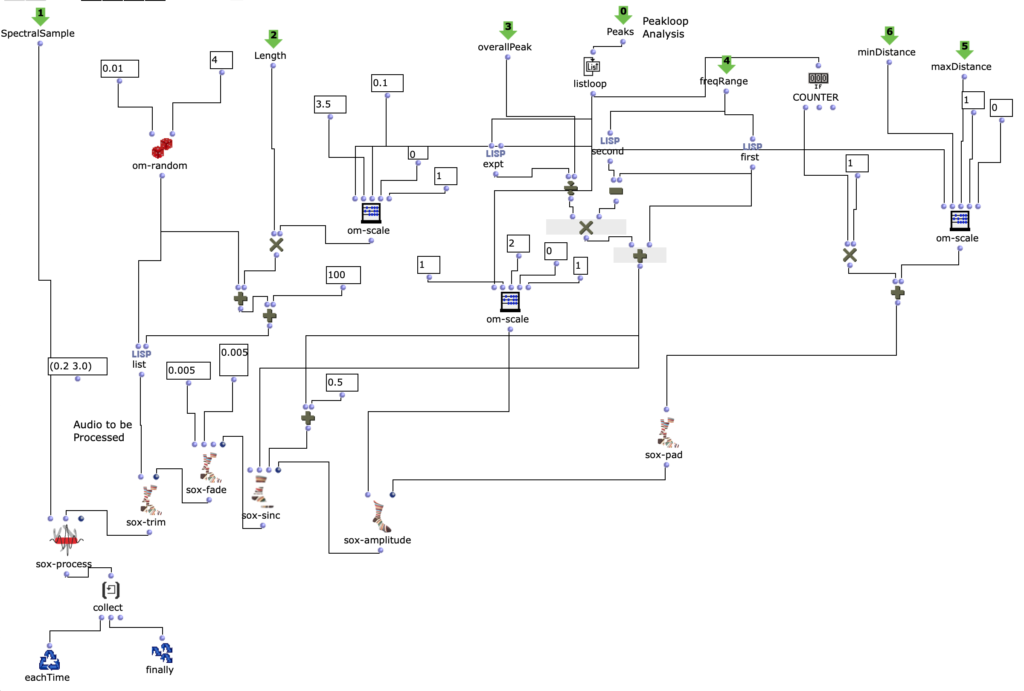
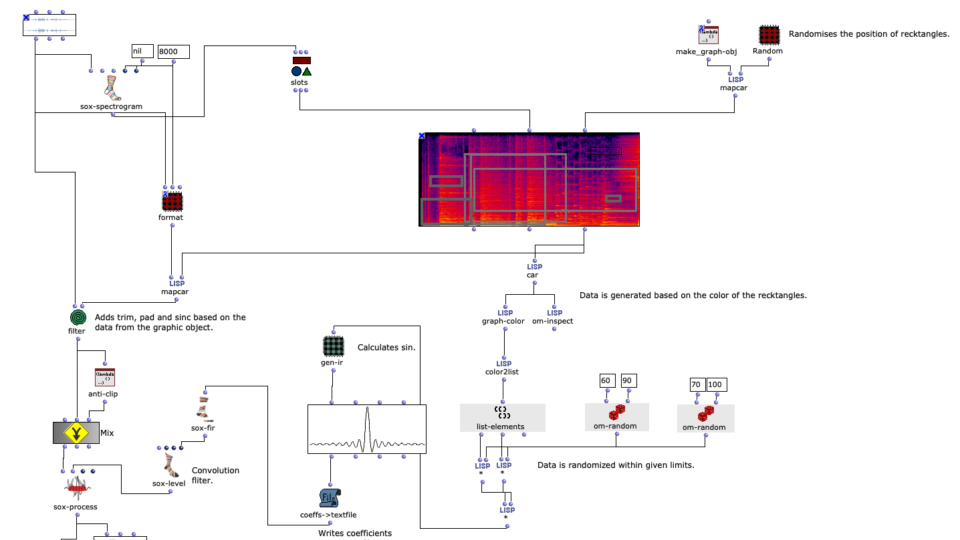
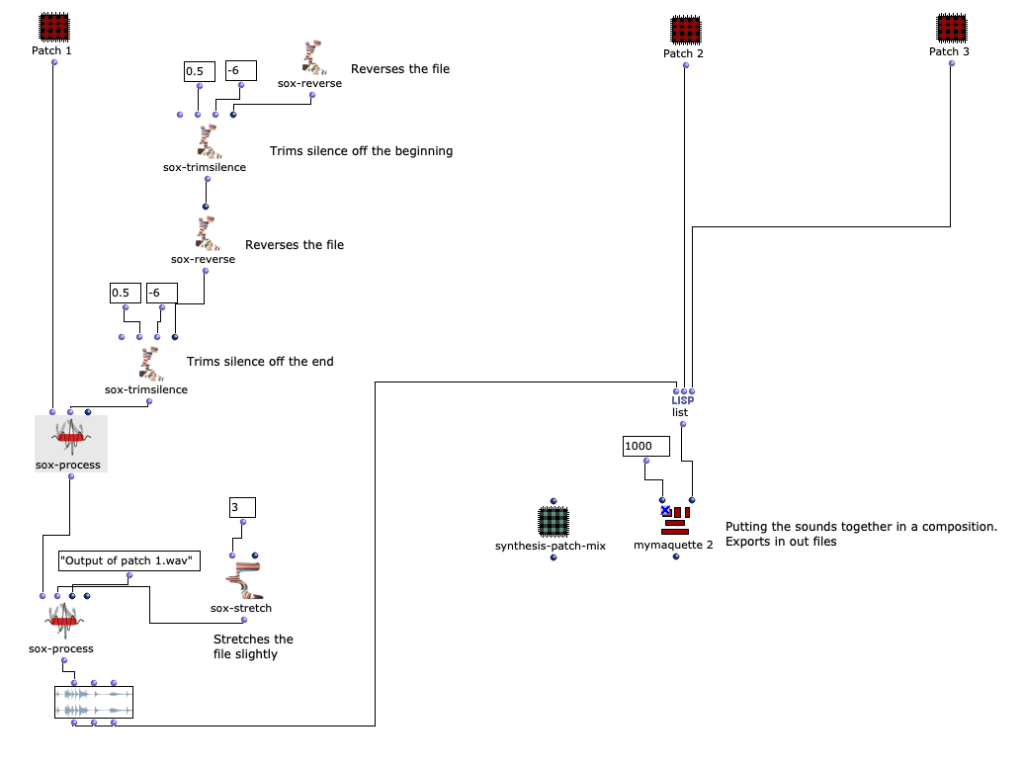
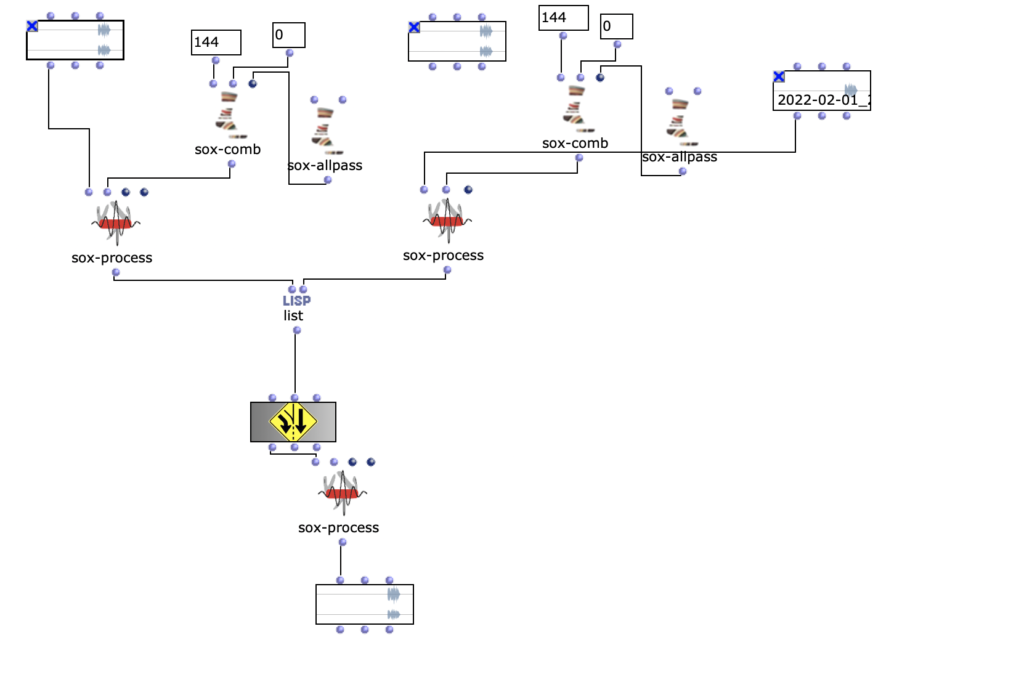
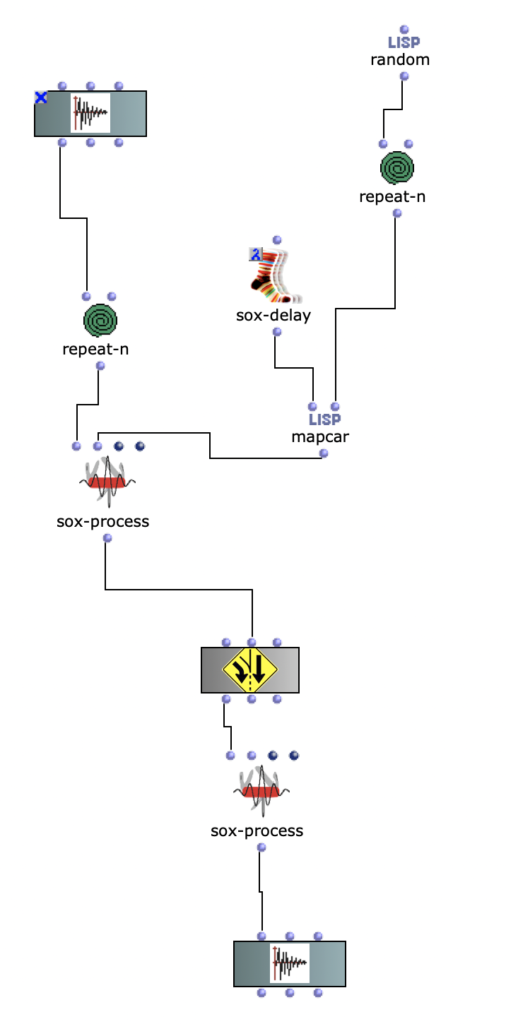
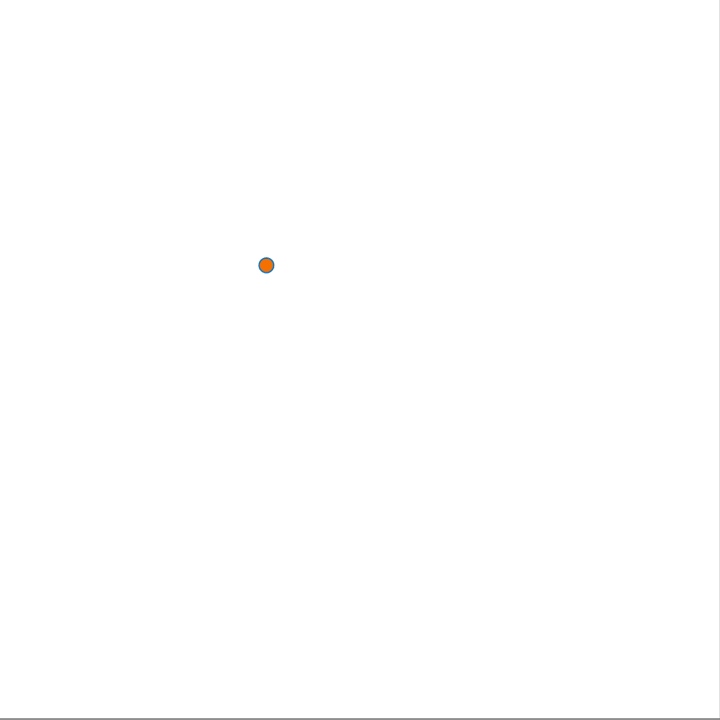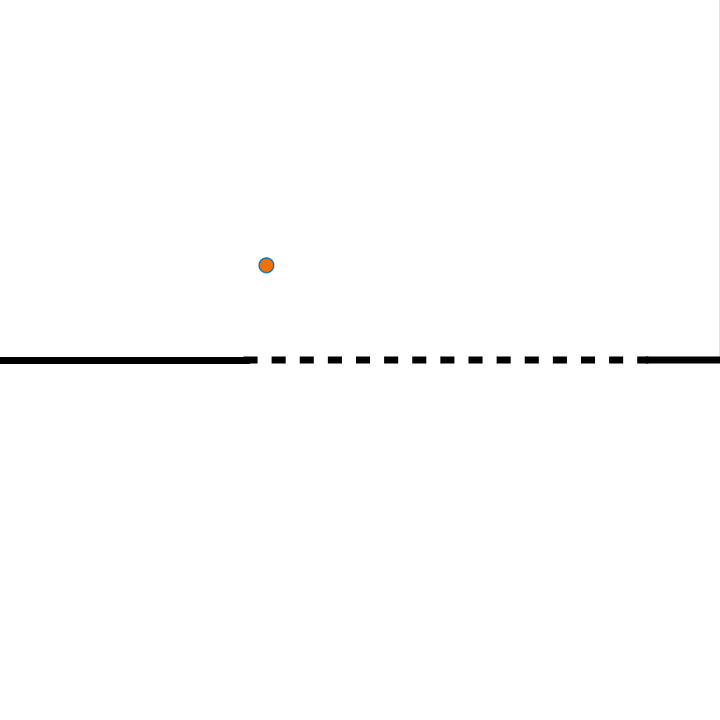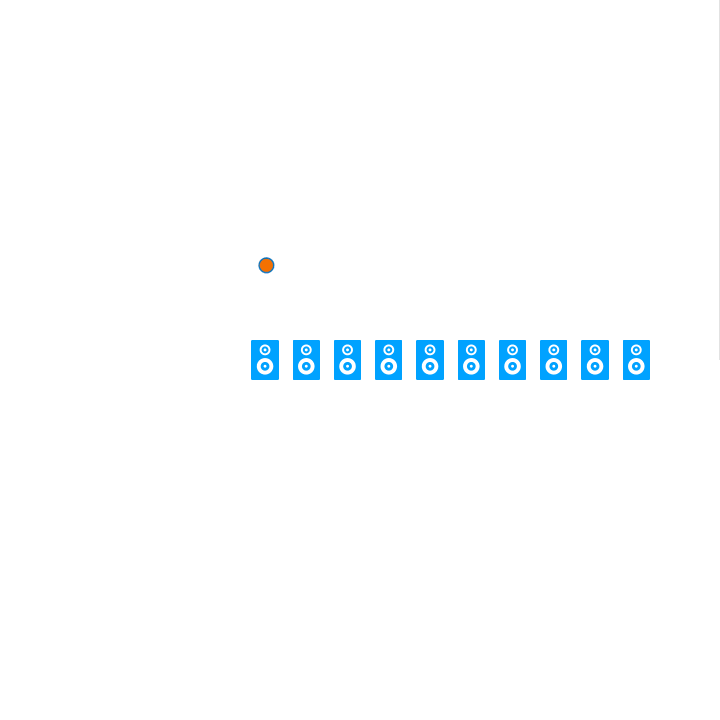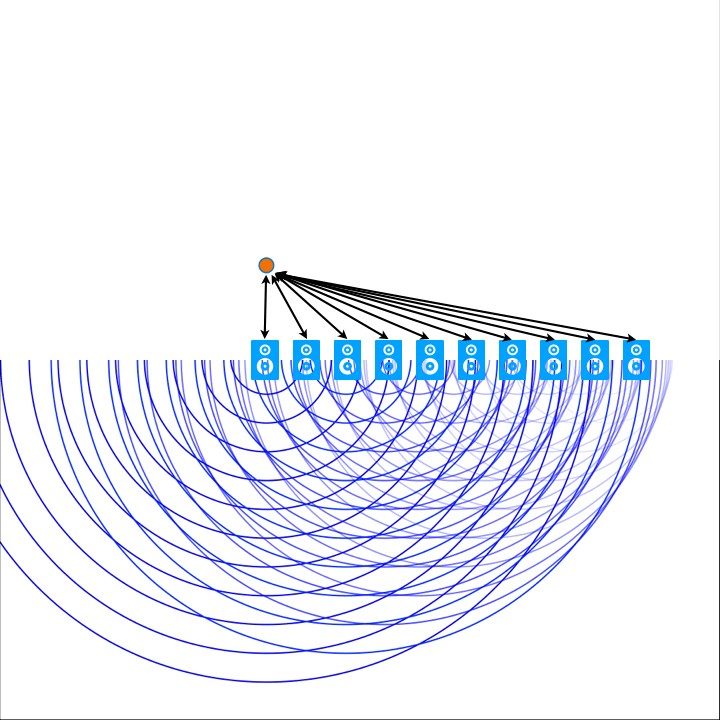Abstract: OpenMusic and the OM-SoX library were used to create a way to encode mono audio files as a 3D Ambisonics signal up to the third order.
Responsible: Alexander Nguyen (WS 2023/24)
Main text:
Ambisonics
Ambisonics is a method for describing a two- or three-dimensional sound field (in the following I shall restrict myself to 3D Ambisonics). Ambisonics uses a basis of orthogonal functions and the spherical coordinate system to describe the sound field along a spherical surface resulting from a sound source . The simplest case is “Zero-th Order Ambisonics”, which resembles an ideal omnidirectional microphone: exactly one audio channel is used (also called the “W” channel, according to Furse-Malham naming). With “First Order Ambisonics” (FOA), the signal is split into an additional three channels (three bases): These are the three “directional” components (also called X, Y, Z channels). Assuming an ideal point sound source is placed at the end of one of these axes, then only this axis (with respect to the same ordinal number) will contain the signal. In the case of Ambisonics, the channels of lower orders are always included, i.e. the FOA signal consists of a total of four audio channels. In general, the number of channels for a 3D Ambisonics signal of the $n$th order can be calculated using the formula $(n+1)^2$ (i.e. for $n=0$: 1; for $n=1$: 4, for $n=2$: 9, for $n=3$: 16). Ambisonics signals with ‘higher’ order numbers (…, 2, 3, 4, …) are also referred to as Higher Order Ambisonics (HOA).
Channel Numbering
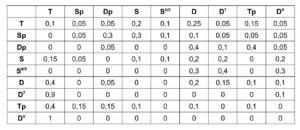
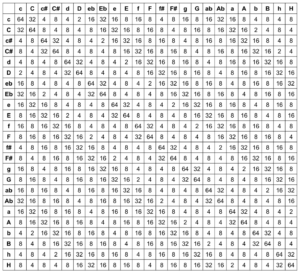
An HOA signal therefore consists of several components. There are several approaches to sorting the components in a multi-channel audio file. The sorting chosen here for this project is “Ambisonic Channel Numbering” (ACN), in which each channel is assigned an integer number starting at zero (0). The first channel is therefore labeled “0”, the second channel “1”, the third channel “2” and so on. This numerical designation can be used to determine the ‘order’ ($l$) and the ‘degree‘ ($m$) to which the component belongs. See Table 1 for an overview of all components of 3rd Order Ambisonics (3OA) – and a collation with an alternative labeling, “Furse Malham” (FuMa).
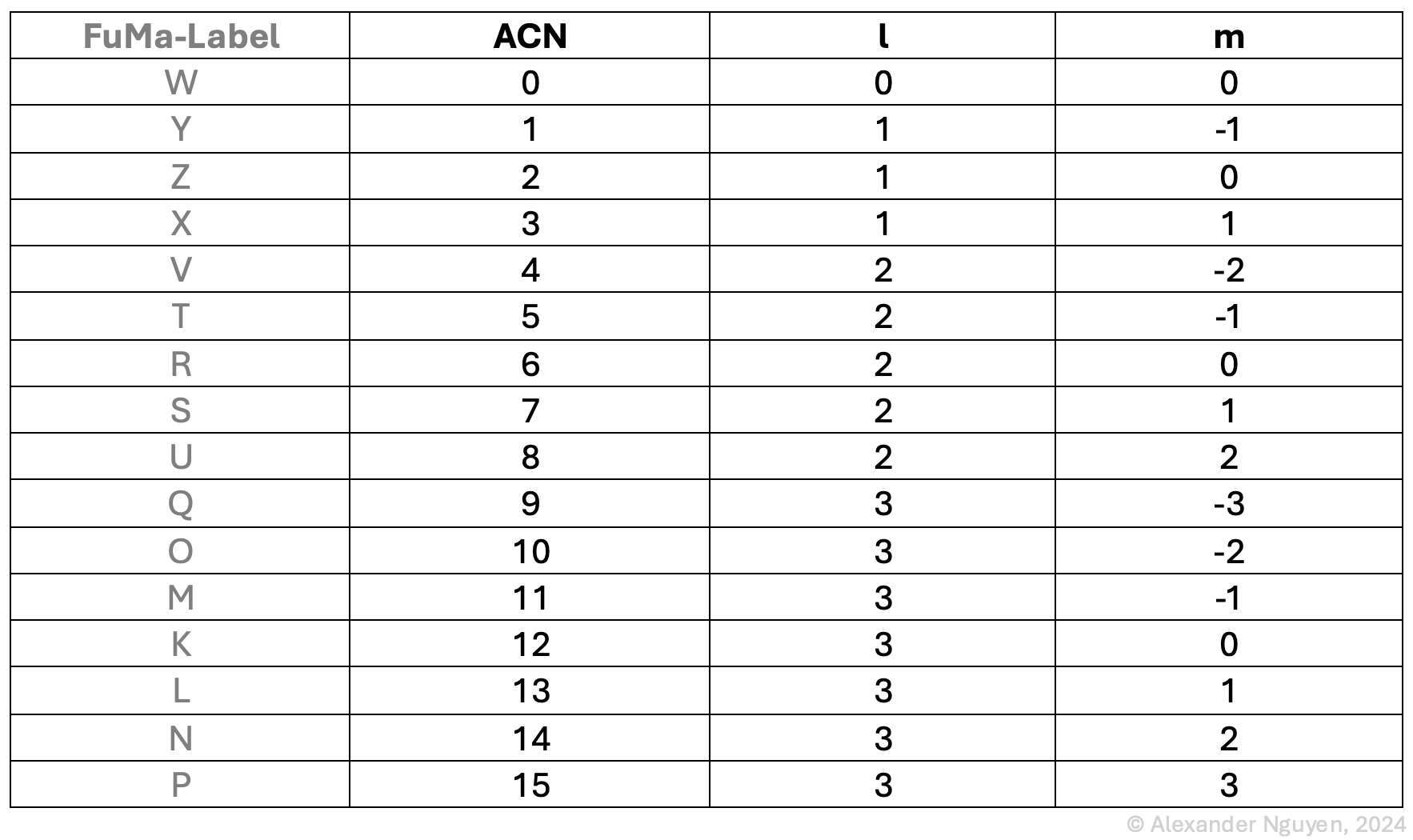
Table 1. Evaluation of the formulas for l and m based on the ACN values. In addition, the alternative designation according to Furse-Malham (FuMa)
Normalization
The values $l$ (order) and $m$ (degree) are used to calculate a normalization factor for each audio channel. The normalization used here is called “Semi-Normalized 3D” (SN3D). See Table 2 for an overview of the normalization factors for all components of 3rd Order Ambisonics.
ACN together with SN3D normalization reflect a currently common convention called ambiX (Nachbar et al., 2011).
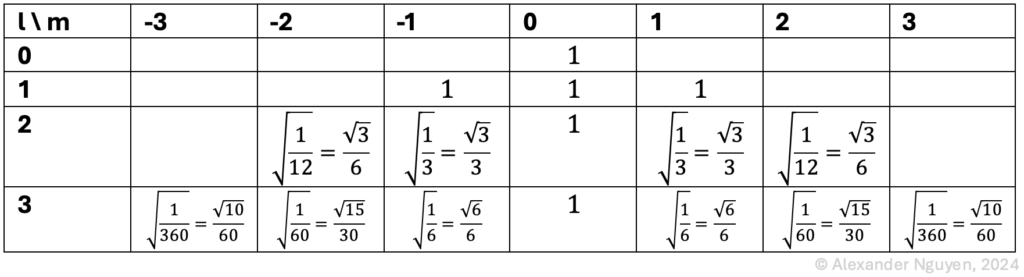
Table 2. SN3D factors for order $l$ and degree $m$, i.e. $N_{lm}^{(SN3D)}$. Note: If $m=0$, then $N_{l0}^{(SN3D)}=1$, and that the table is symmetric with respect to $±m$.
Encoding
To map a point sound source in Ambisonics, its audio signal is added to each of the audio channels, weighted using the normalization factor just described and an attenuation factor. The attenuation factor, which will be defined below, depends on the angle of incidence (described in the spherical coordinate system) and the ACN number (i.e. order and degree). An intuition (w.r.t. FOA): The attenuation is minimum (0 dB or multiplication factor 1, respectively) if the angle of incidence coincides with one of the axes in an ordinary 3-dimensional coordinate system ($x$, $y$ or $z$), maximum (-∞ dB or factor 0) if it is perpendicular to it.
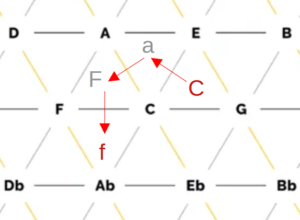
In Ambisonics, the 3D coordinate system is usually defined as follows: The “front” (relative to the listener’s point of view) is defined as the positive x-axis. Being a right-handed system, this implies that the positive y-axis points to the “left” and the positive z-axis points “up“. For the transformation to polar coordinates, i.e. to the spherical coordinate system, one defines 0° azimuth (θ) coincident to the positive x-axis on the xy-plane, counterclockwise. 0° elevation (ϕ) coincident to the xy-plane, maximum positive, if coincident to the positive z-axis (see Figure 1), with:
$0≤θ≤2π$
$-π/2≤ϕ≤π/2$
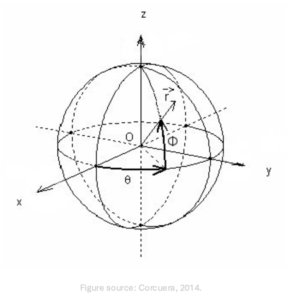
Figure 1. Visualization of the coordinate system and the reference points. Positive-x = front, positive-y = left, positive-z = top. θ (theta) left-turning (0° = front), ϕ “up-turning” (0° = in the xy plane).
In order to encode a time $t$-dependent signal $S(t)$ of a point sound source with angles of incidence $θ, ϕ$ in Ambisonics, the eventual Ambisonics signal component is calculated separately for each channel $B_l^m$. To do this, the signal is multiplied by the attenuation factor $Y_l^m$ :
$B_l^m (t) := S(t)\cdot Y_l^m (\theta, \phi)$
The formula for the attenuation factor is (see Nachbar et al., 2011):
\[
Y_l^m(\theta, \phi) :=N_l^{|m|} \cdot P_l^{|m|}(sin(\phi)) \cdot \begin{cases}
sin(|m|\theta) & \text{if } m < 0\\
cos(|m|\theta) & \text{if } m > 0\\
1 & \text{if } m=0
\end{cases}
\]
where $P_l^m$ is the “associated Legendre polynomial” of $l$-th order and $m$-th degree, and $P_l$ is the (unassociated) Legendre polynomial of $l$-th order (in the Rodrigues representation). These are defined as follows:
\[\begin{eqnarray*}
P_l(x) &:=& \frac{1}{2^l\cdot l!}\cdot \frac{d^l}{dx^l} \left[ (x^2-1)^l \right] \\
P_l^m(x) &:=& (1-x^2)^{\frac{m}{2}}\cdot \frac{d^m}{dx^m} \left[ P_l(x) \right] \\
&=& \frac{1}{2^l\cdot l!}\cdot (1-x^2)^\frac{m}{2}\cdot\frac{d^{l+m}}{dx^{l+m}} \left[ (x^2-1)^l \right]
\end{eqnarray*}\]
For example:
\[\begin{eqnarray*}
P_0^0(x) &=& (1-x^2)^\frac{0}{2}\cdot \frac{d^0}{dx^0} \left[ P_0(x) \right] \\
&=& 1\cdot P_0(x) = 1 \cdot 1 = 1
\end{eqnarray*}\]
\[\begin{align*}
P_2^1(x) &= (1-x^2)^\frac{1}{2}\cdot \frac{d^1}{dx^1} \left[ P_2(x) \right] \\
&= (1-x^2)^\frac{1}{2}\cdot \frac{d}{dx} \left[ \frac{1}{2^2\cdot 2!}\cdot \frac{d^2}{dx^2} [ (x^2-1)^2 ] \right] \\
&= (1-x^2)^\frac{1}{2}\cdot \frac{d}{dx} \left[ \frac{1}{8}\cdot \frac{d^2}{dx^2} [ x^4-2x^2+1 ] \right] \\
&= (1-x^2)^\frac{1}{2}\cdot \frac{d}{dx} \left[ \frac{1}{8}\cdot \frac{d}{dx} [ 4x^3-4x ] \right] \\
&= (1-x^2)^\frac{1}{2}\cdot \frac{d}{dx} \left[ \frac{1}{8}\cdot [ 12x^2-4 ] \right] \\
&= (1-x^2)^\frac{1}{2}\cdot \frac{d}{dx} \left[ \frac{3}{2} x^2 -\frac{1}{2} \right] \\
&= (1-x^2)^\frac{1}{2}\cdot \left[ \frac{3\cdot 2}{2} x \right] \\
&= (1-x^2)^\frac{1}{2}\cdot \frac{6}{2}x \\
&= 3x\cdot (1-x^2)^\frac{1}{2} \\
\end{align*}\]
Let $x≡sin(ϕ)$, then we obtain one of the spherical harmonics (see Table 3 for further examples):
\[\begin{align*}
P_2^1(sin(\theta)) &= 3\cdot sin(\phi)\cdot \sqrt{1-sin^2(\phi)} \\
&= 3\cdot sin(\phi)\cdot \sqrt{cos^2(\phi)} \\
&= 3\cdot sin(\phi)\cdot cos(\phi) \\
&= \frac{3\cdot sin(2\phi)}{2} \\
\end{align*}\]
The formulas for FOA are thus:
\[\begin{align*}
\text{ACN 1 / W:}\qquad &B_0^0(t) =S(t)\cdot Y_0^0(\theta, \phi)= S(t) \\
\text{ACN 2 / Y:}\qquad &B_1^{-1}(t) =S(t)\cdot Y_1^{-1}(\theta, \phi)= S(t)\cdot cos(\phi) \cdot sin(\theta) \\
\text{ACN 3 / Z:}\qquad &B_1^0(t) =S(t)\cdot Y_1^1(\theta, \phi)= S(t)\cdot sin(\phi) \\
\text{ACN 4 / X:}\qquad &B_1^1(t) =S(t)\cdot Y_1^1(\theta, \phi)= S(t) \cdot cos(\phi) \cdot cos(\theta) \\
\end{align*}\]

Table 3. Ambisonics formulas up to third order (ACN counting, SN3D normalization, $0≤θ≤2π$ azimuth (0° = forward, counterclockwise), $-π/2≤ϕ≤π/2$ elevation (0° = on the xy plane, upward rotation))