Abstract: Ein Projekt über den Einsatz von Zufallsprozessen in einem musikalischen Kontext. Grundsätzlich kommen zwei verschiedene Modelle zum Einsatz. Diese erzeugen Akkordfolgen, welche anschließend mit einem Rhythmus und einer darüber liegenden Melodie ausgestattet werden.
Verantwortliche: Moritz Reiser
Überblick
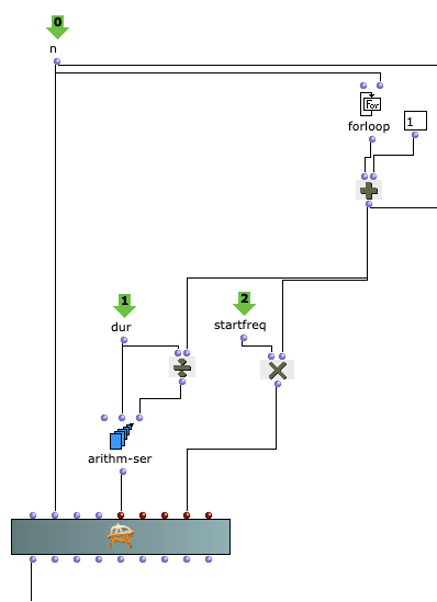
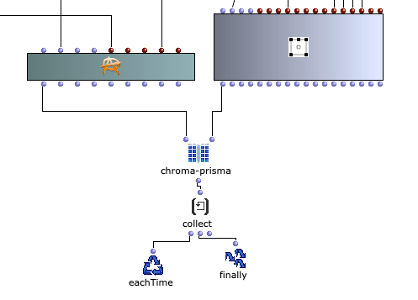
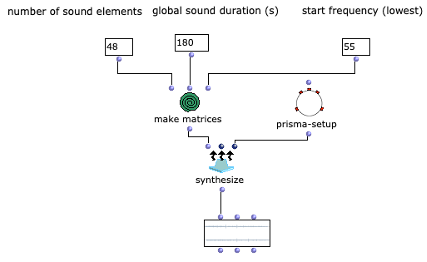
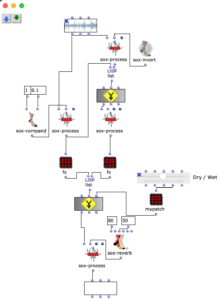
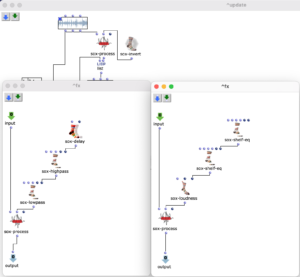
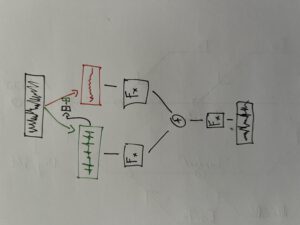
Der Gesamtaufbau des Programms, welcher dem Inhalt des Hauptpatches entspricht, ist in Abbildung 1 zu sehen. Ganz oben befindet sich die Auswahl des zu verwendenden Algorithmus zur Akkordfolgenerzeugung. Über das Auswahlfeld links oben kann dieser ausgewählt werden. Durch die beiden Inputfelder der Subpatches lassen sich jeweils die gewünschte Länge sowie der Startakkord bzw. die Tonart der Komposition festlegen.
Anschließend folgt eine zufällige Bestimmung der jeweiligen Tonlängen. Hier lassen sich das Tempo in BPM sowie die Häufigkeiten der vorkommenden Tonlängen in Vielfachen von Viertelnoten einstellen. Über eine „dx→x“-Funktion werden aus den berechneten Dauern die jeweiligen Startzeitpunkte der Akkorde berechnet. Hier muss beim Verwenden des Programms darauf geachtet werden, dass Open Music aufgrund des zweimal verwendeten Outputs in den beiden Strängen jeweils neue Zufallszahlen berechnet, wodurch der Bezug zwischen Startzeitpunkt und Tondauer verloren geht. Abhilfe kann hier dadurch geschaffen werden, dass nach einmaliger Ausführung die Subpatches der Akkordfolgen- und der Tonlängengenerierung mit „Lock Eval“ gesperrt werden und das Programm anschließend noch einmal ausgeführt wird, um die Startzeitpunkte an die nun gespeicherten Tondauern anzupassen (siehe Hinweistafel im Hauptpatch). Der dritte große Schritt des Gesamtablaufs besteht schließlich in der Generierung einer Melodie, die über der Akkordfolge liegt. Hier wird jeweils ein Ton aus dem zugrunde liegenden Akkord ausgewählt und eine Oktave nach oben verschoben. Dabei kann eingestellt werden, ob dies immer ein zufälliger Akkordton sein soll, oder ob der Ton gewählt wird, welcher dem vorangehenden Melodieton am nächsten bzw. am weitesten entfernt ist.
Das Resultat wird schließlich ganz unten in einem Multi-Seq-Objekt visualisiert.
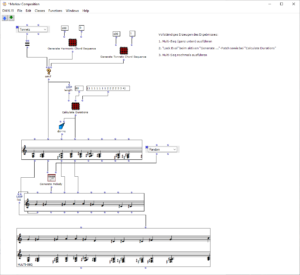
Abbildung 1: Gesamtaufbau des Kompositionsprozesses
Akkordfolgengenerierung
Zur Generierung der Akkordfolge stehen zwei Algorithmen zur Verfügung. Ihnen wird jeweils die gewünschte Länge der Sequenz, welcher der Anzahl der Akkorde entspricht, und der Startakkord bzw. die Tonart übergeben.
Harmonische Akkordfolge mittels Markovkette
Der Ablauf des ersten Algorithmus ist in Abbildung 2 zu sehen. Durch den Subpatch „Create Harmonic Chords“ wird der Grundvorrat von Akkorden erzeugt, der im Folgenden verwendet wird. Dieser entspricht den üblichen Stufen der Kontrapunktlehre und enthält neben Tonika, Subdominante, Dominante und deren Parallelen einen verminderten Akkord auf der siebten Stufe, einen Sixte ajoutée der Subdominante und einen Dominantseptakkord. Der „Key“-Input addiert zu diesen Akkorden einen der gewünschten Tonart entsprechenden Wert hinzu.
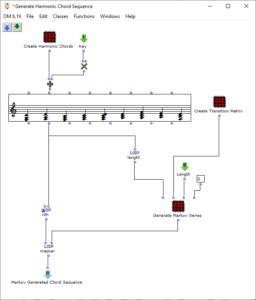
Abbildung 2: Subpatch zur Generierung einer harmonischen Akkordsequenz mithilfe einer Markovkette
Durch den Subpatch „Create Transition Matrix“ wird eine Matrix mit Übergangswahrscheinlichkeiten der einzelnen Akkorde erzeugt. Für jede Akkordstufe wird festgelegt, mit welcher Wahrscheinlichkeit sie zu einem bestimmten anderen Akkord übergeht. Die Wahrscheinlichkeitswerte wurden hierbei willkürlich gemäß den in der Kontrapunktlehre üblichen Abläufen gewählt und experimentell angepasst. Dabei wurde für jeden Akkord untersucht, wie wahrscheinlich aus diesem jeweils in einen anderen Akkord übergegangen wird, sodass das Resultat den Konventionen der Kontrapunklehre entspricht und eine häufige Rückkehr zur Tonikastufe ermöglicht, um diese zu fokussieren. Die exakten Übergangswahrscheinlichkeiten sind in der folgenden Tabelle aufgelistet, wobei die Ausgangsklänge in der linken Spalte aufgelistet sind und die Übergänge jeweils zeilenweise repräsentiert werden.
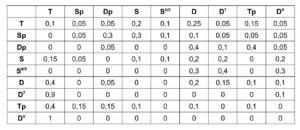
Tabelle 1. Übergangswahrscheinlichkeiten der Harmonien entsprechender Akkordstufen
Die Erzeugung der Akkordfolge findet schließlich in dem Patch „Generate Markov Series“ statt, welcher in Abbildung 3 dargestellt ist. Dieser arbeitet zunächst nur mit Nummerierungen der Akkordstufen, weshalb es genügt, ihm die Länge des Akkordvorrats zu übergeben. Die Lisp-Funktion „Markov Synthesis“ erzeugt nun mithilfe der Übergangsmatrix eine Akkordfolge der gewünschten Länge. Da bei der so erzeugten Sequenz nicht sichergestellt ist, dass der letzte Akkord der Tonika entspricht, kommt eine weitere Lisp-Funktion zum Einsatz, welche so lange weitere Akkorde generiert, bis die Tonika erreicht ist. Da bisher nur mit Nummerierungen der Stufen gearbeitet wurde, werden abschließend die für die jeweiligen Stufen gültigen Akkorde ausgewählt, um die fertige Akkordfolge zu erhalten.
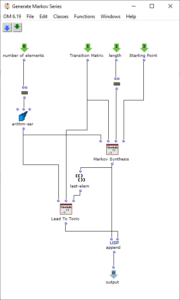
Abbildung 3: Subpatch zur Erzeugung einer Akkordfolge mittels Markovsynthese
Chromatische Akkordfolge mittels Tonnetz
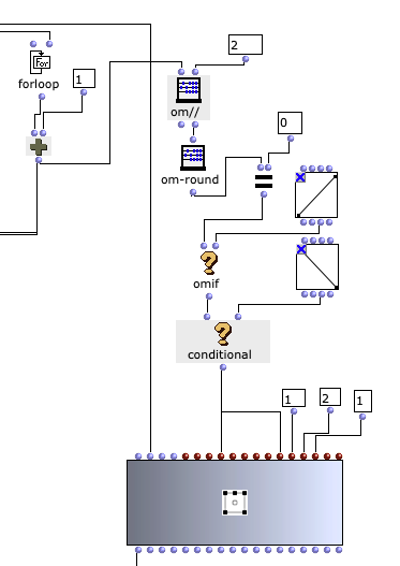
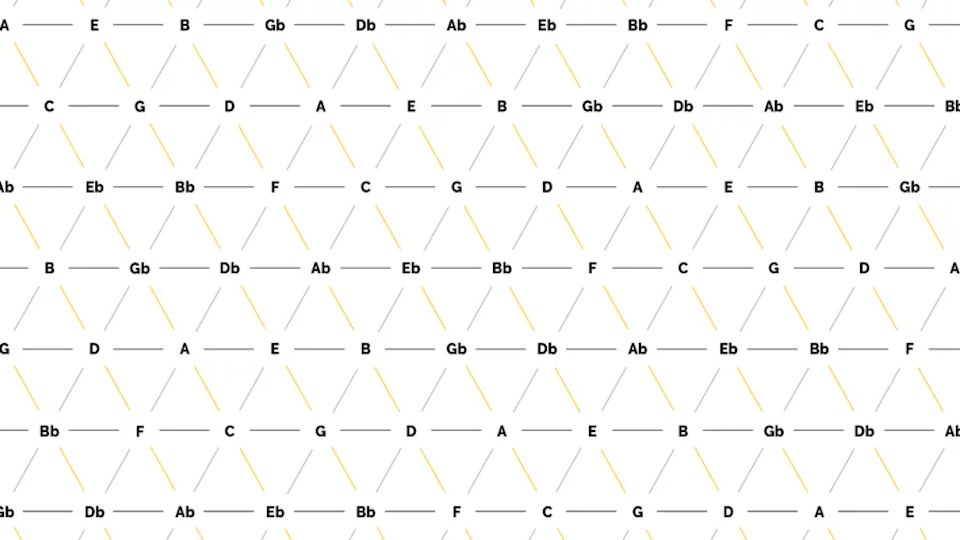
Im Gegensatz zur harmonischen Akkordfolge kommen hier alle 24 Dur- und Mollakkorde der chromatischen Skala zum Einsatz (siehe Abbildung 4). Die Besonderheit dieses Algorithmus liegt in der Wahl der Übergangswahrscheinlichkeiten. Diese basieren auf einem sogenannten Tonnetz, welches in Abbildung 5 dargestellt ist.
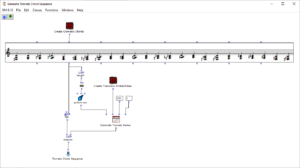
Abbildung 4: Subpatch zur Generierung einer Akkordfolge auf Basis der Tonnetz-Darstellung
Innerhalb des Tonnetzes sind einzelne Töne aufgetragen und miteinander verbunden. Auf den horizontalen Linien haben die Töne jeweils den Abstand einer Quinte, auf den diagonalen Linien sind kleine (von links oben nach rechts unten) sowie große Terzen (von links unten nach rechts oben) zu sehen. Die sich so ergebenden Dreiecke repräsentieren jeweils einen Dreiklang, beispielsweise ergibt das Dreieck der Töne C, E und G den Akkord C-Dur. Insgesamt sind so alle Dur- und Moll-Akkorde der chromatischen Skala zu finden. Zum Einsatz kommt die Tonnetz-Darstellung meist zu Analyse-Zwecken, da sich aus einem Tonnetz direkt ablesen lässt, wie viele Töne sich zwei verschiedene Dreiklänge teilen. Ein Beispiel ist die Analyse von klassischer Musik der Romantik und Moderne sowie von Filmmusik, da hier die oben verwendeten harmonischen Kontrapunktregeln häufig zu Gunsten von chromatischen und anderen zuvor unüblichen Übergängen vernachlässigt werden. Der Abstand zweier Akkorde im Tonnetz kann hierbei ein Maß dafür sein, ob der Übergang des einen Akkords in den anderen wohlklingend oder eher ungewöhnlich ist. Er berechnet sich aus der Anzahl von Kanten, die überquert werden müssen, um von einem Akkord-Dreieck zu einem anderen zu gelangen. Anders ausgedrückt entspricht er dem Grad der Nachbarschaft zweier Dreiecke, wobei sich eine direkte Nachbarschaft durch das Teilen einer Kante ergibt. Abbildung 6 zeigt hierzu ein Beispiel: Um ausgehend vom Akkord C-Dur zum Akkord f-Moll zu gelangen, müssen drei Kanten überquert werden, wodurch sich ein Abstand von 3 ergibt.
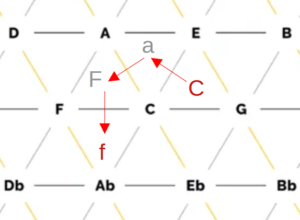
Abbildung 6: Beispiel der Abstandsbestimmung im Tonnetz anhand des Übergangs von C-Dur nach f-Moll
Im Rahmen des Projekts werden nun die Übergangswahrscheinlichkeiten auf Basis der Abstände von Akkorden im Tonnetz berechnet. Hierbei muss lediglich unterschieden werden, ob es sich bei dem jeweils aktiven Dreiklang um einen Dur- oder Mollakkord handelt, da sich innerhalb dieser beiden Klassen für alle Tonarten dieselben Abstände zu anderen Akkorden ergeben. Dadurch kann jeder Übergang von C-Dur bzw. c-Moll aus berechnet und anschließend durch Addition eines Wertes in die gewünschte Tonart verschoben werden. Von beiden Varianten (C-Dur und c-Moll) ausgehend wurden zunächst die Abstände zu allen anderen Dreiklängen im Tonnetz festgehalten:
Abstände von C-Dur:

Abstände von c-Moll:

Um aus den Abständen Wahrscheinlichkeiten zu erhalten wurden zunächst alle Werte von 6 abgezogen, um größere Abstände unwahrscheinlicher zu machen. Anschließend wurden die Resultate als Exponent der Zahl 2 verwendet, um nähere Akkorde stärker zu gewichten. Insgesamt ergibt sich somit die Formel
P=2^(6-x) ; P=Wahrscheinlichkeit, x=Abstand im Tonnetz
zur Berechnung der Übergangsgewichtungen. Diese ergeben sich für alle möglichen Akkordkombinationen zu folgender Matrix, aus welcher bei Division durch die Zeilensumme 342 Wahrscheinlichkeiten resultieren.
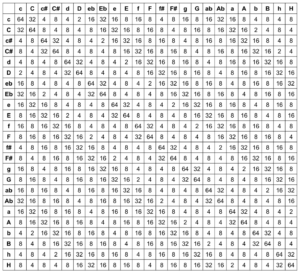
Innerhalb des Patches stellt die Lisp-Funktion „Generate Tonnetz Series“ zunächst jeweils fest, ob es sich bei dem aktiven Akkord um einen Dur- oder Molldreiklang handelt. Da wie bei der harmonischen Vorgehensweise zunächst nur mit den Zahlen 0-23 gearbeitet wird, kann dies über eine einfache Modulo-2-Rechnung bestimmt werden. Je nach Resultat wird der jeweilige Wahrscheinlichkeiten-Vektor herangezogen, ein neuer Akkord bestimmt und schließlich die vorherige Stufe hinzuaddiert. Ergibt sich eine Zahl, die größer als 23 ist, wird 24 abgezogen, um immer innerhalb der selben Oktave zu bleiben.
Nach der zuvor festgelegten Länge der Sequenz ist dieser Abschnitt beendet. Auf eine Rückführung zur Tonika wie im vorherigen Abschnitt wird hier verzichtet, da aufgrund der Chromatik keine so stark ausgeprägte Tonika vorherrscht wie bei der harmonischen Akkordfolge.
Bestimmung der Tonlängen
Nach der Generierung einer Akkordfolge werden für die einzelnen Dreiklänge zufällige Längen berechnet. Dies geschieht im Subpatch „Calculate Durations“, der in Abbildung 6 dargestellt ist. Neben der gewünschten BPM-Zahl wird ein Vorrat an Tonlängen als Vielfache von Viertelnoten übergeben. Wahrscheinlichere Werte kommen in diesem Vorrat häufiger vor, sodass über „nth-random“ eine entsprechende Wahl getroffen werden kann.
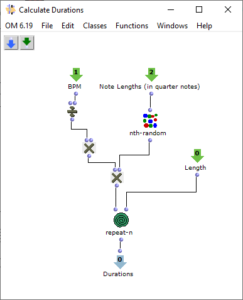
Abbildung 7: Subpatch zur zufälligen Bestimmung der Tondauern
Melodiegenerierung
Der grundsätzliche Ablauf der Melodiegenerierung wurde oben bereits dargestellt: Aus dem jeweiligen Akkord wird ein Ton ausgewählt und um eine Oktave nach oben transponiert. Dieser Ton kann zufällig oder entsprechend dem kleinsten oder größten Abstand zum Vorgängerton gewählt werden.
Klangbeispiele
Beispiel für eine harmonische Akkordfolge:
Beispiel für eine Tonnetz-Akkordfolge: