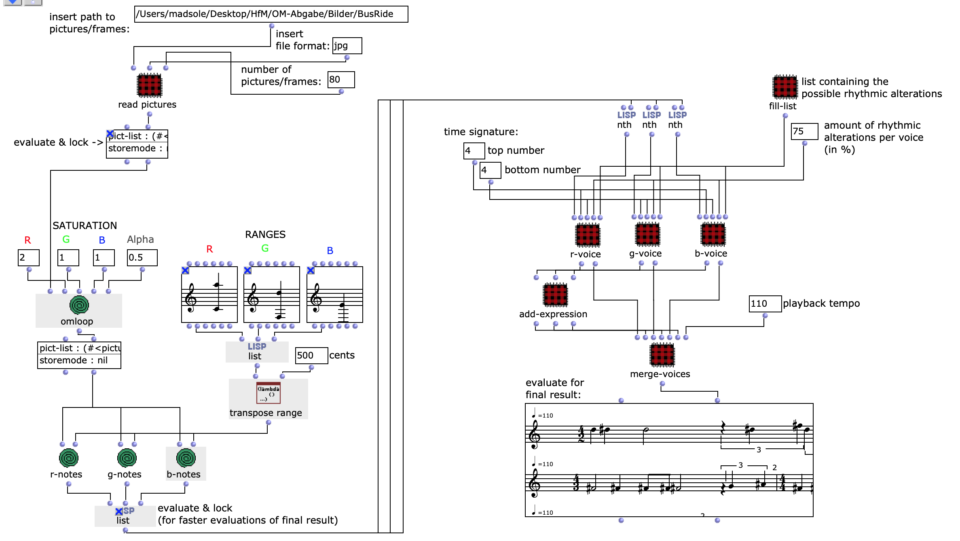
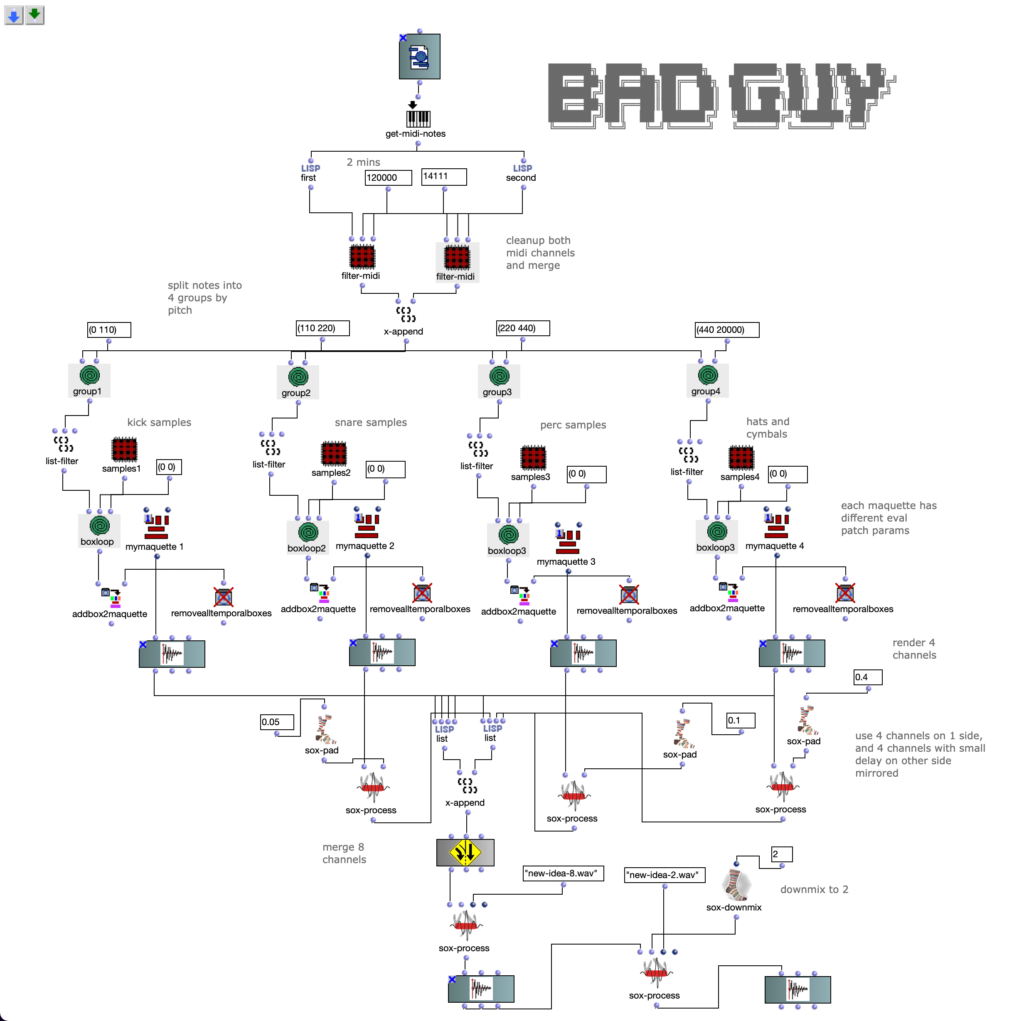
Abstract: Dieses Projekt beschäftigt sich mit dem Entwurf einer OpenMusic Anwendung, die die Umwandlung von Bildsequenzen in eine symbolische Musikrepräsentation, bestehend aus drei Stimmen, zur Aufgabe hat.
Verantwortliche: Mads Clasen
Ausgangsmaterial und Vorbereitung
Bei der Bildsequenz kann es sich um einzelne Frames eines Videos, eine Bilderserie eine Künstlers oder selbst zusammengestellte Bilder handeln. Diese müssen zunächst in einem Ordner auf dem entsprechenden Rechner vorliegen. Sollte es sich um ein Video handeln, muss dieses, außerhalb von OpenMusic, zuvor in seine Frames zerlegt werden. In Python ist dies mit Hilfe von OpenCV innerhalb weniger Zeilen ganz unkompliziert durchführbar.
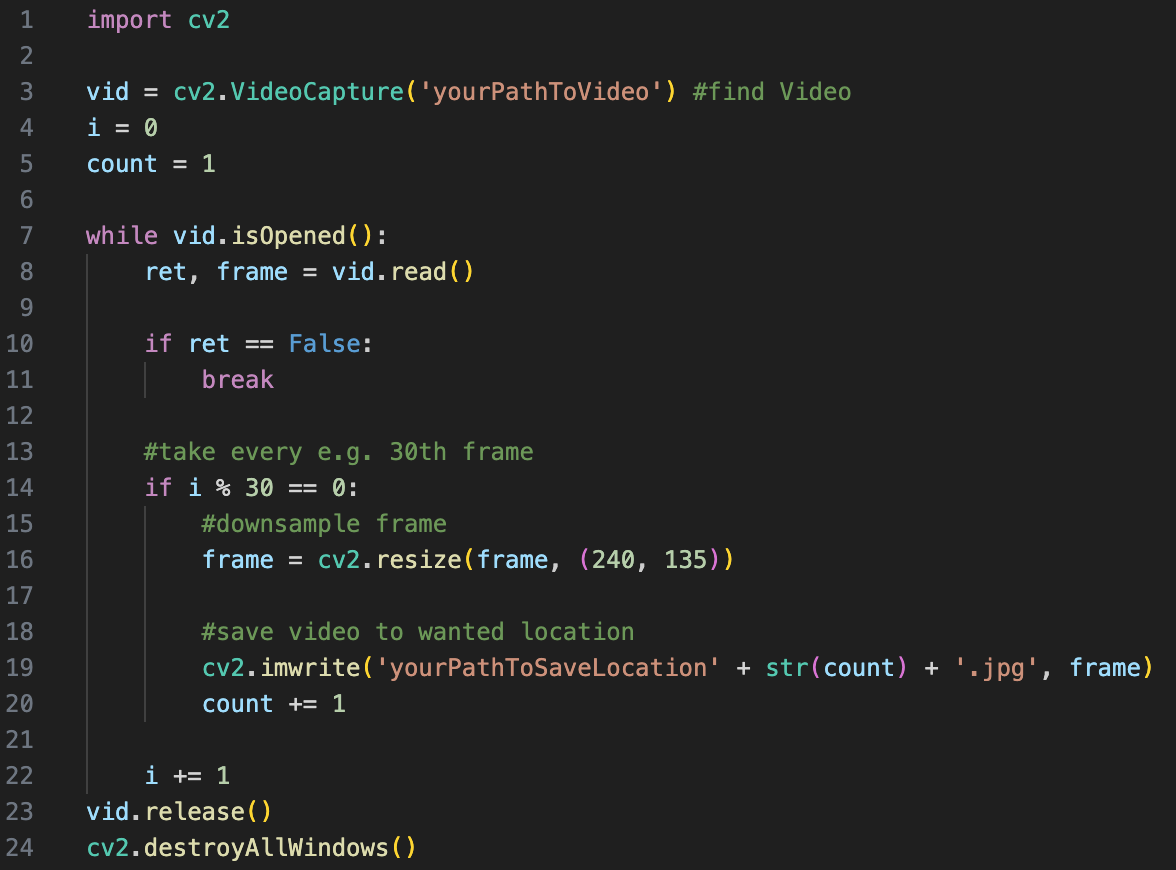
Abb. 1: Zerlegen von Video in Python
Wie im Codebeispiel zu sehen, sollten die resultierenden Bilder außerdem numerisch mit Zahlen von 1 bis n benannt werden und, abhängig von Rechenleistung des Rechners und Bildmenge, downgesampled werden. Dies ist für die korrekte Funktionsweise des Patches von Nöten, sowie in OpenMusic selbst die Installation der Pixels Library.
Sonifikation
Notenwerte
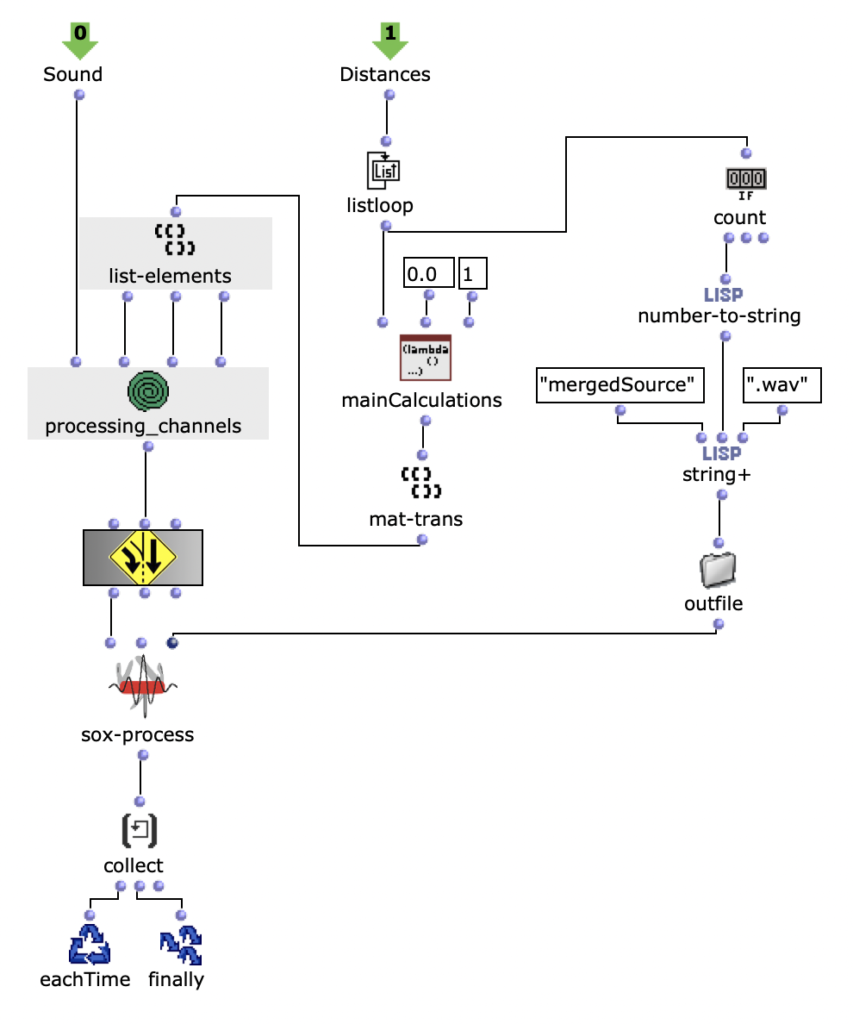
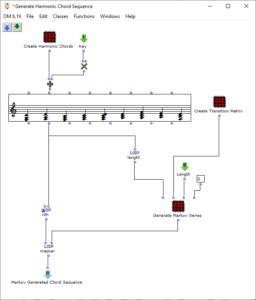
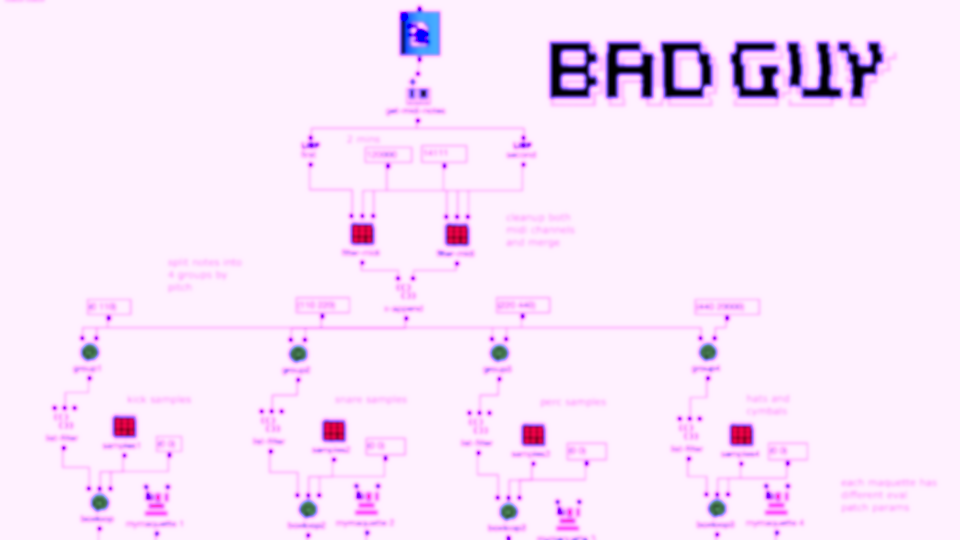
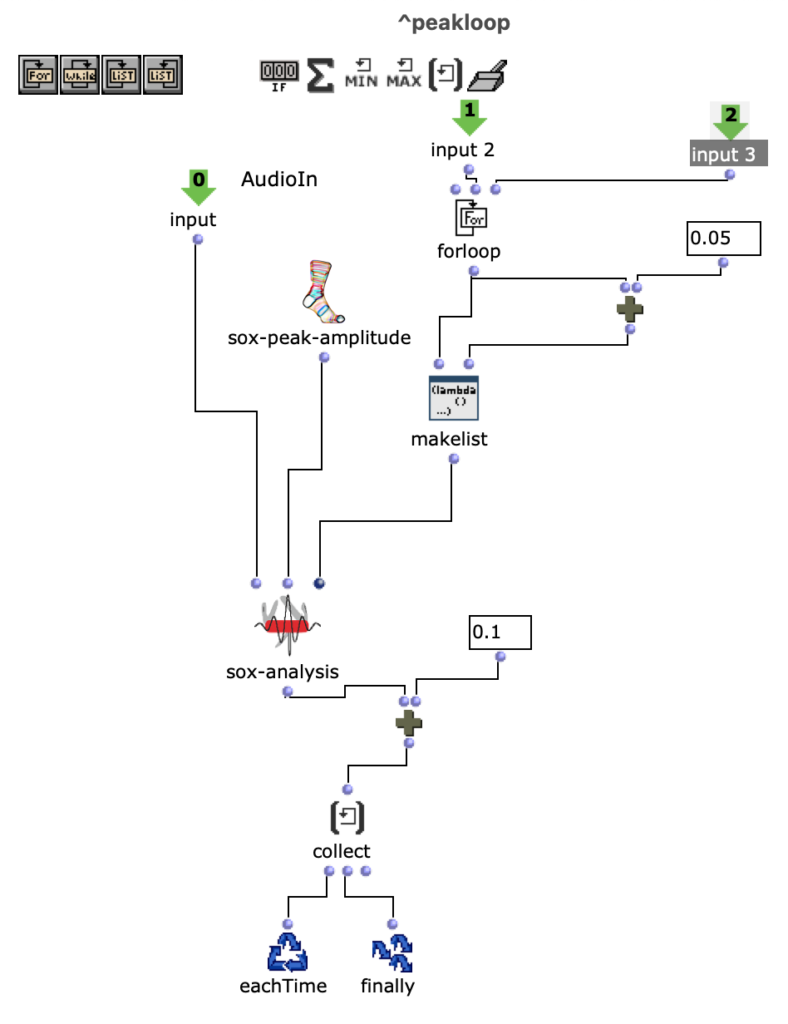
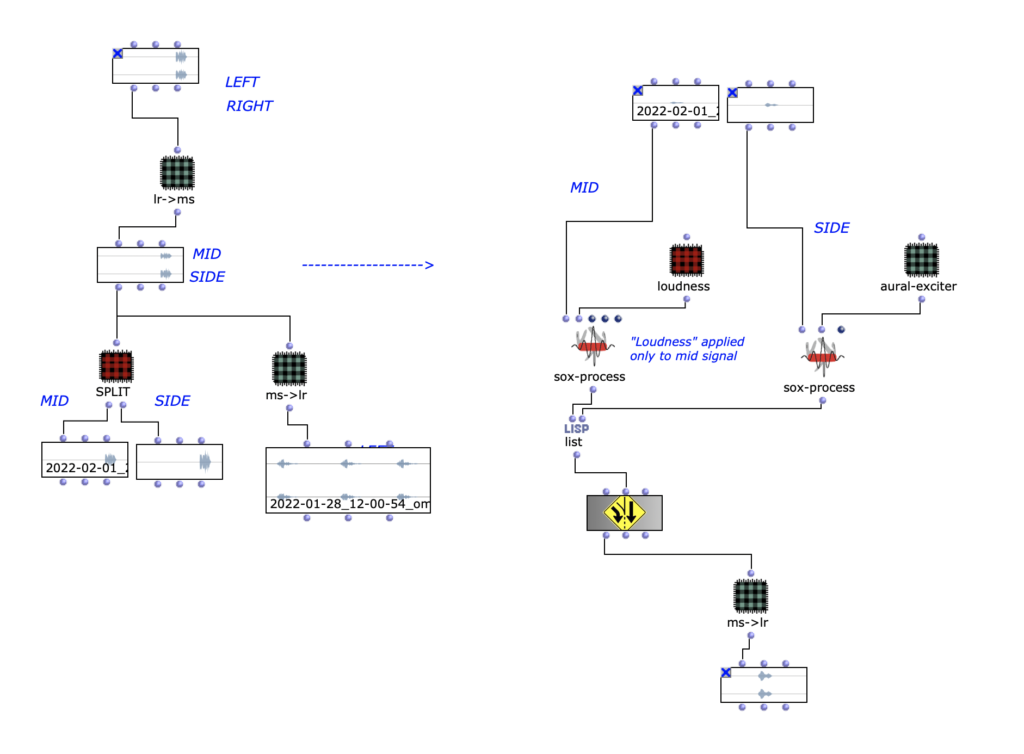
Die gewünschten Bilder werden, nach Angabe von Dateipfad, Dateiformat und Anzahl der Bilder, in ein picture-lib Objekt geladen und als Liste zusammengefasst. Aus jedem Bild dieser Liste wird der jeweils durchschnittliche R, G und B Farbwert ausgelesen und auf eine dementsprechende Note gemappt. In diesem Fall werden die R, G und B Werte wie unterschiedliche Stimmen behandelt und verfügen jeweils über eine eigene Notenrange innerhalb derer sie sich bewegen. Diese ist zusätzlich in mikrototale Schritte (1/8 Töne) unterteilt, auf welche die Werte schlussendlich gemaEin Wert von 1 entspricht dabei der höchsten möglichen Noten und 0 der tiefsten. Dementsprechend wird aus einem Bild jeweils eine Note für jede der drei Stimmen ausgelesen.
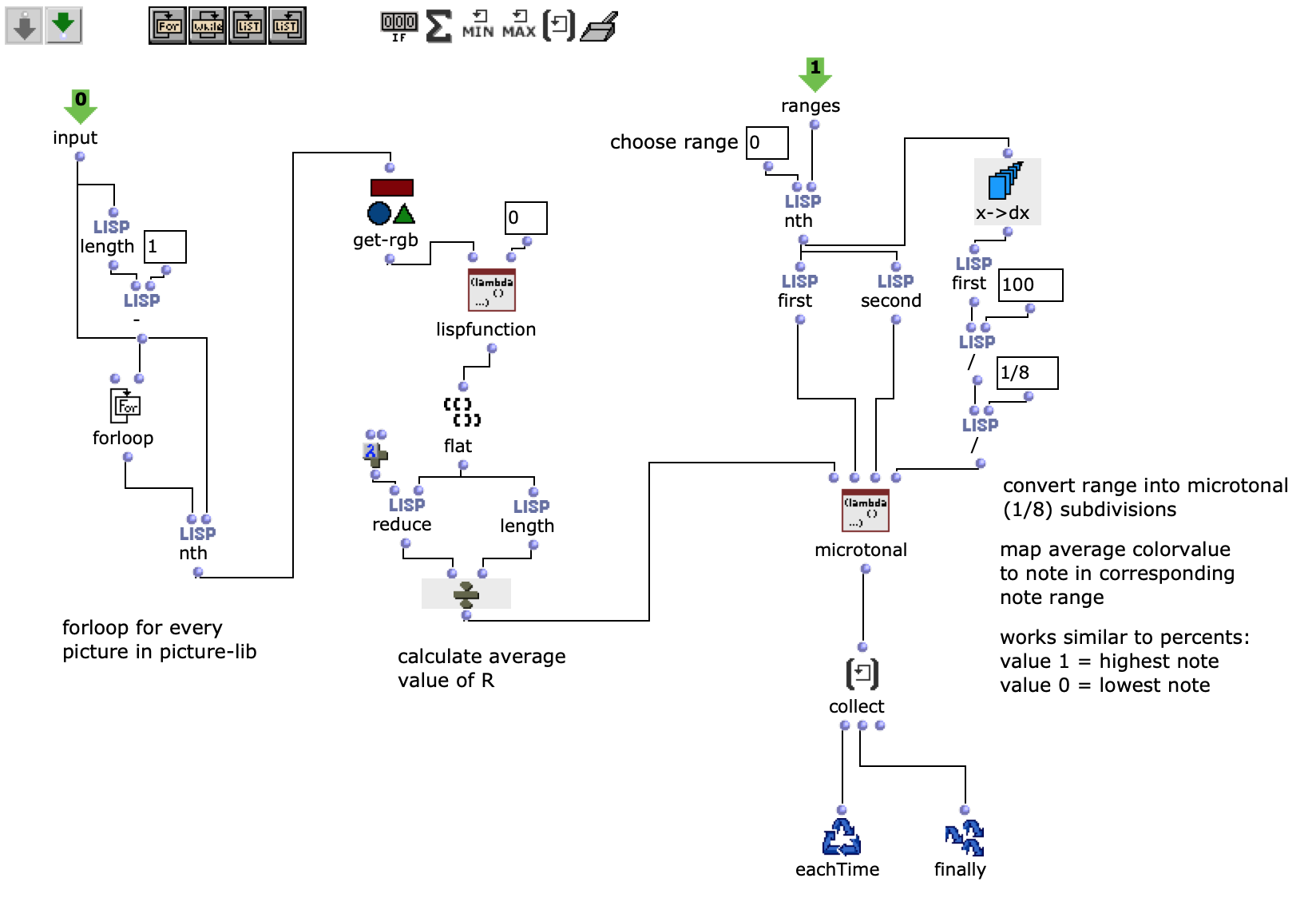
Abb. 2: Generierung einer Notenlinie
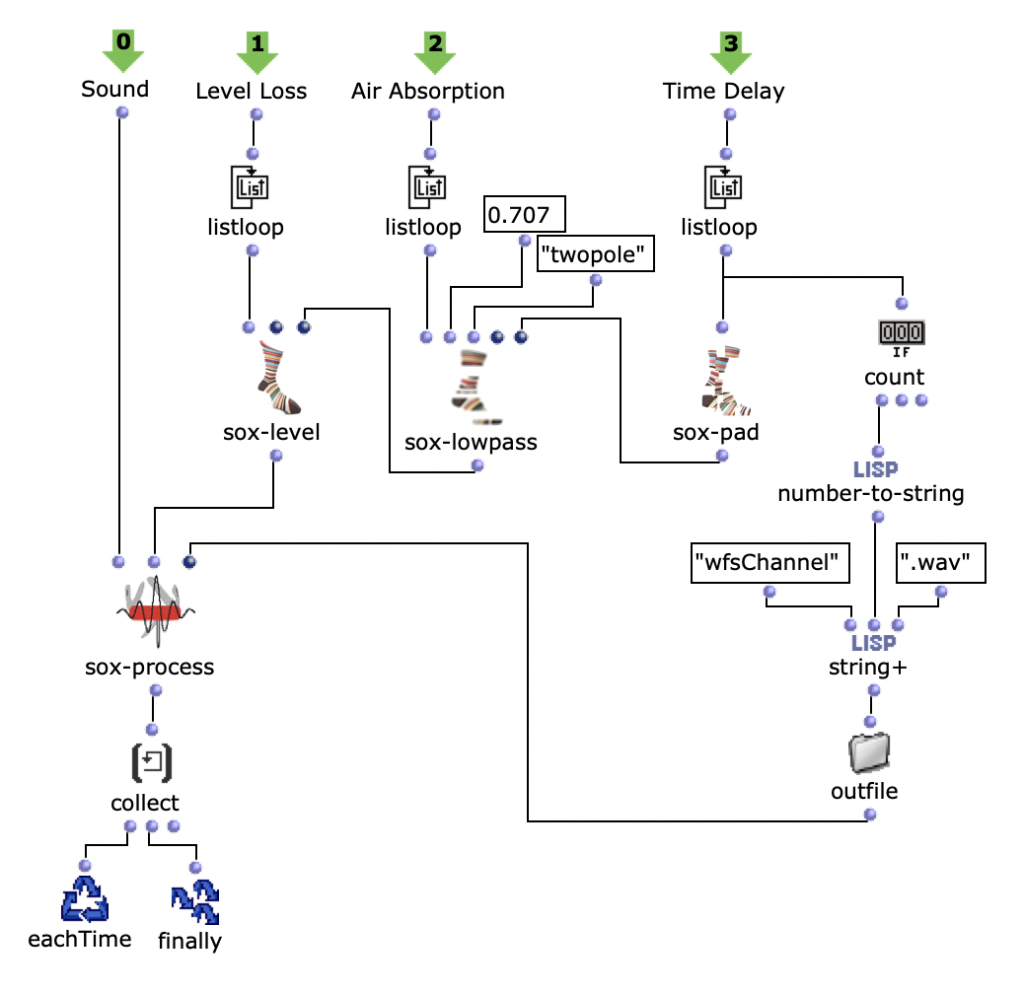
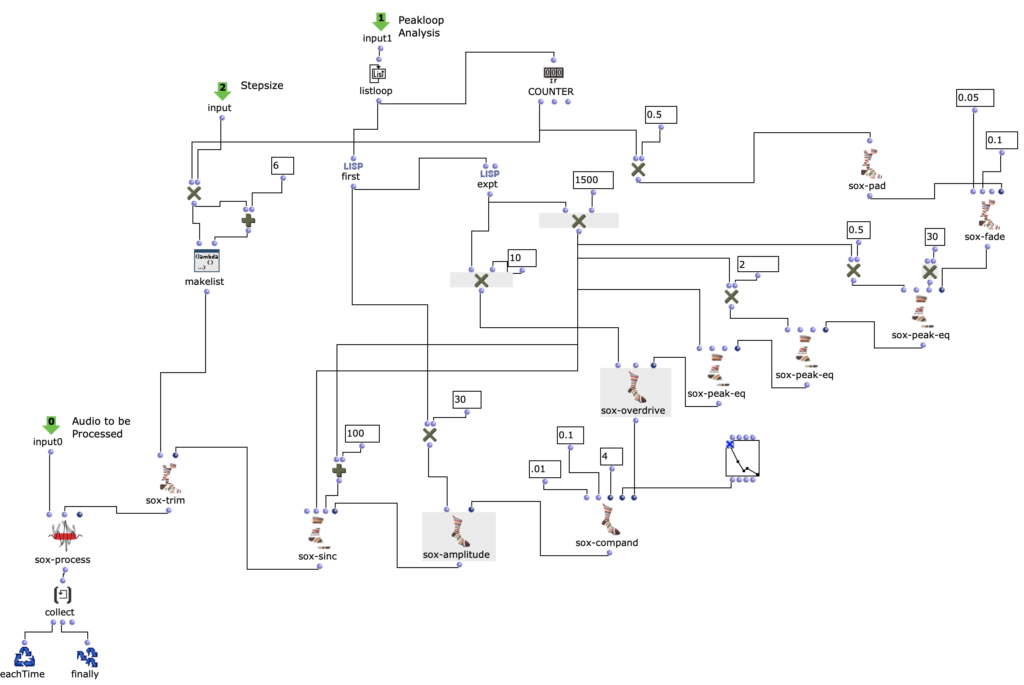
Die Notenranges in denen sich die Farbwerte bewegen, können anhand der entsprechenden chord Objekte angepasst werden, zudem ist die einheitliche Transposition aller Ranges um einen gewünschten Wert in midicents möglich. Die Voreingestellten Werte entsprechen den ungefähren Notenumfängen von Sopran (R), Alt (G) und Bass (B) Stimmen. Nach Durchlauf der gesamten Bildsequenz bestehen nun also drei Stimmen mit einer Notenanzahl entsprechend der Menge an eingegebenen Bildern. Diese Stimmen werden im nächsten Schritt unabhängig voneinander weiterverarbeitet.
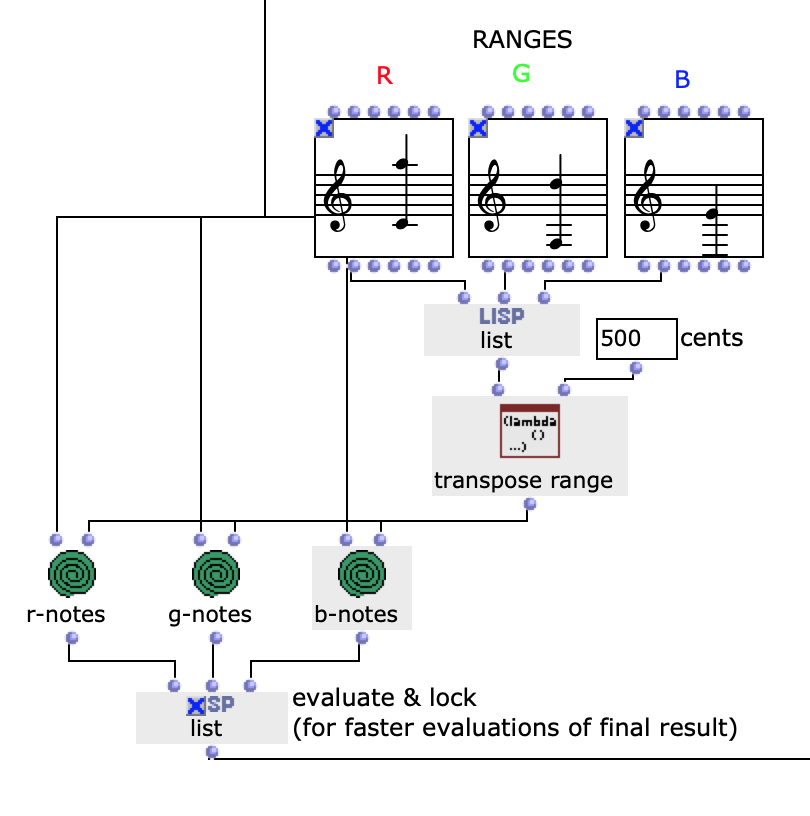
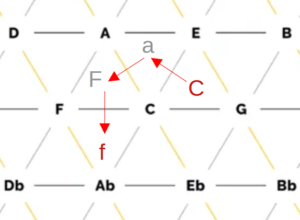
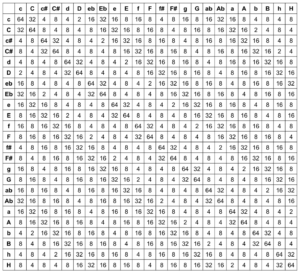
Abb. 3: Mapping der RGB-Werte auf Notenwerte
Rhythmik
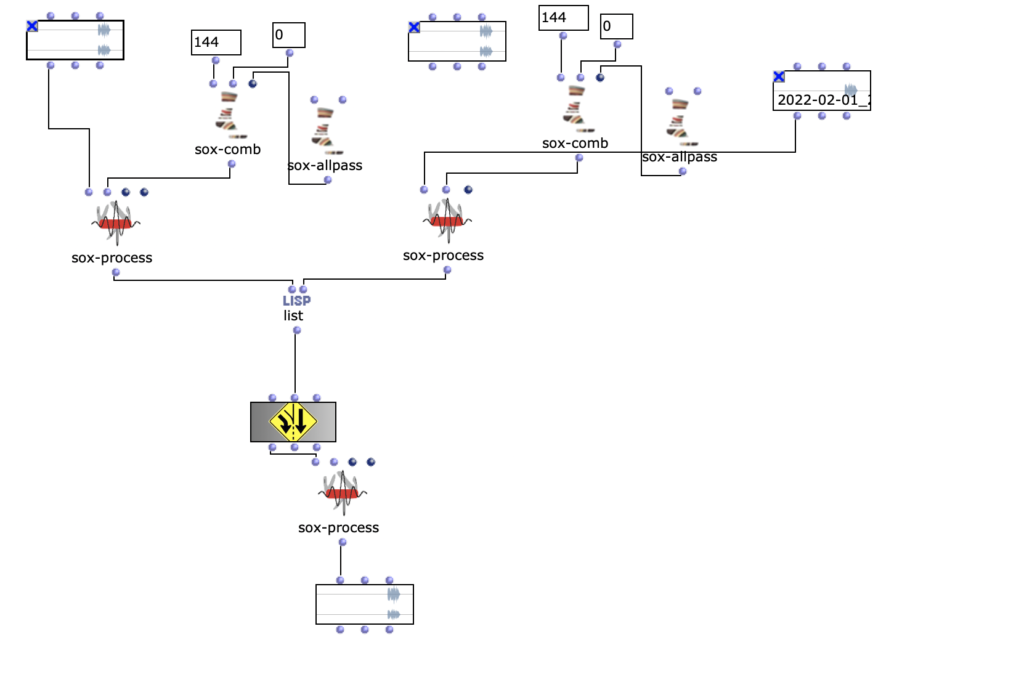
Da ich mich dazu entschieden habe voice Objekte zu nutzen, aufgrund der direkten Art der Einflussnahme auf Rhythmik, werden zunächst die dafür nötigen rhythm trees erzeugt. Beziehungsweise die zwei Bausteine eines rhythm trees : Taktart und Proportionen. Für beide wird jeweils eine Liste erstellt, die sich an der Anzahl der Noten und der eingestellten Taktart orientieren und die später mithilfe eines simplen mat-trans Objektes in die benötigte rhythm tree Form zusammengeführt werden.
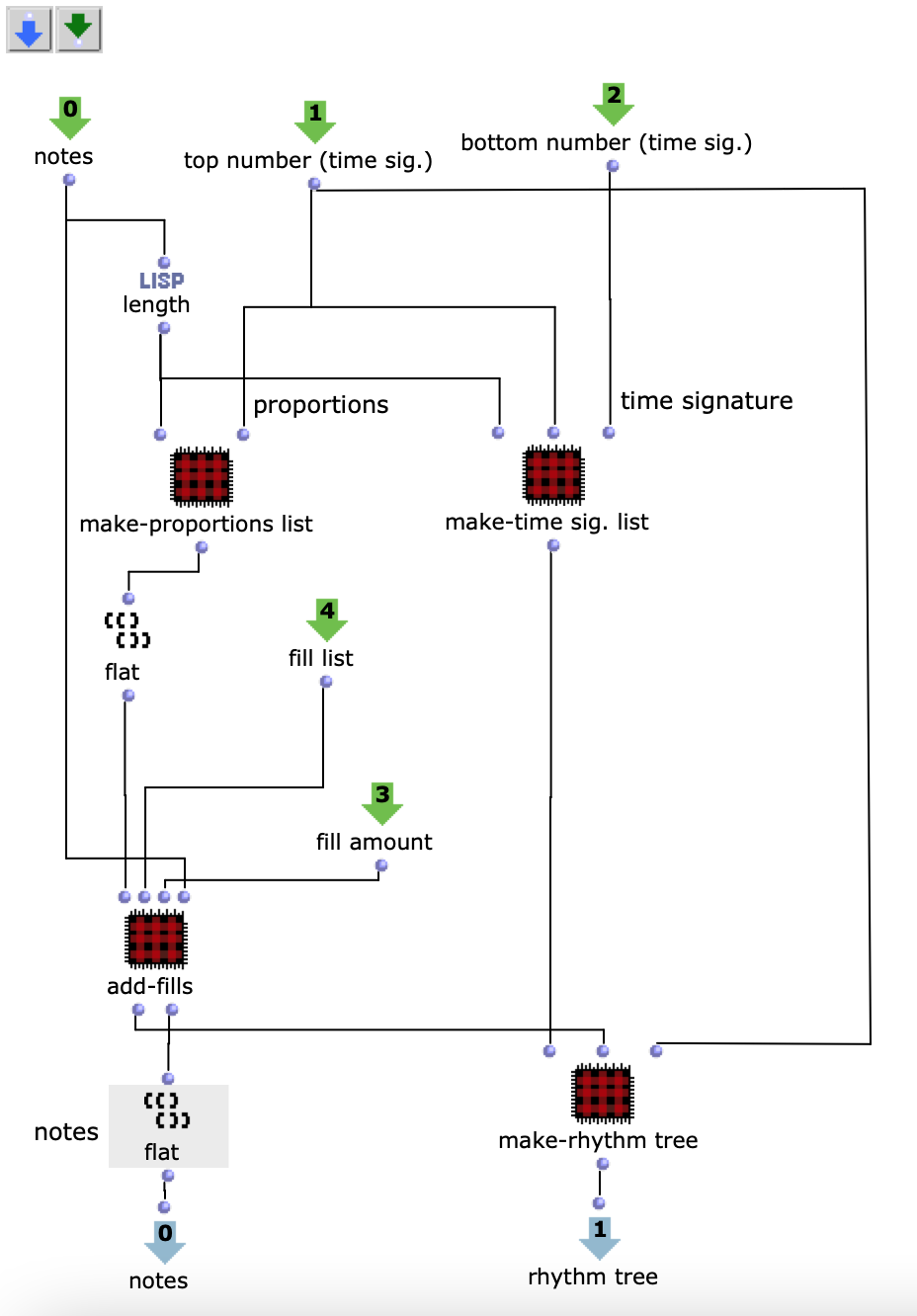
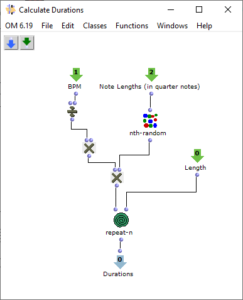
Abb. 4: Generierung rhythm tree
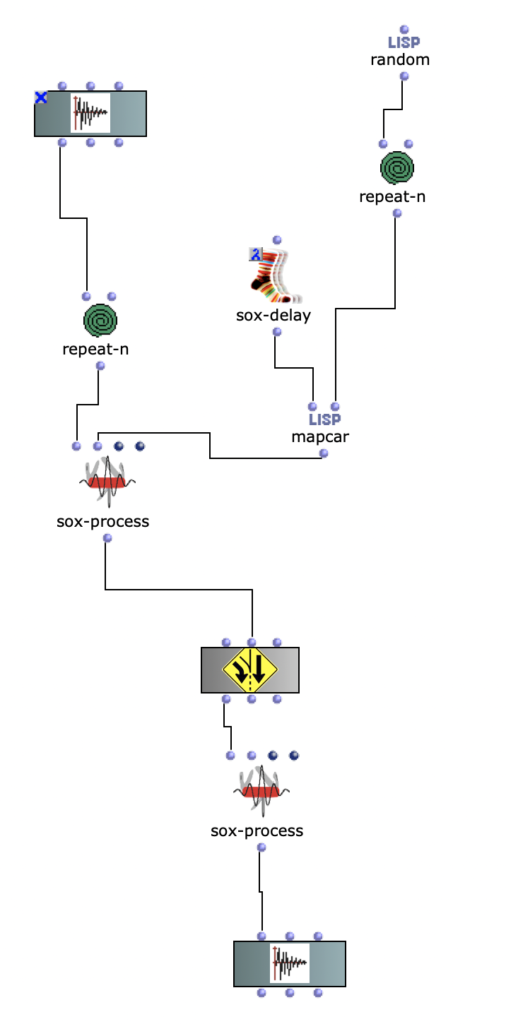
Zuvor wird jedoch die, für die Proportionen zuständige, Liste mit Ostinati angereichert. Dafür gibt es eine zweite Liste, welche verschiedene Möglichkeiten solcher Ostinati beinhaltet, aus der ein zufälliges ausgewählt und an eine ebenfalls zufällige Stelle der Proportionsliste gesetzt wird. Da sich somit die Anzahl der Notenwerte erhöht, werden auch an dieselbe Stelle der, die Noten beinhaltenden, Liste, neue, der Verzierung entsprechende, Noten eingesetzt. Dabei wird, von der Originalnote ausgehend, zwischen gleichbleibenden, auf- oder absteigenden Noten entschieden. Die Stärke, mit der diese Verzierungen Einzug in die Stimmen erhalten sollen, kann zusätzlich angepasst werden.
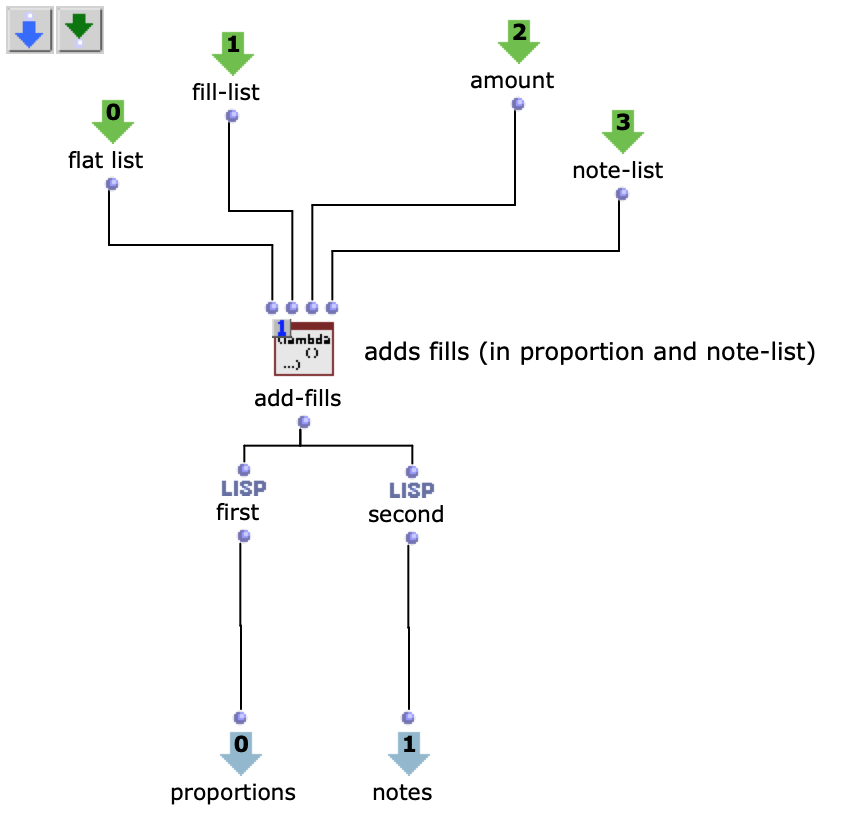
Abb. 5: Ergänzung rhythmischer Verzierungen
Dynamik
Die bearbeiteten Proportionen werden nun anschließend mit der, die Taktart bestimmenden, Liste zum rhythm tree zusammengeführt. Die entsprechende Notenliste durchläuft noch einen Schritt mehr, in welchem jeder Note ein zufälliger Velocity Wert zugeordnet wird.
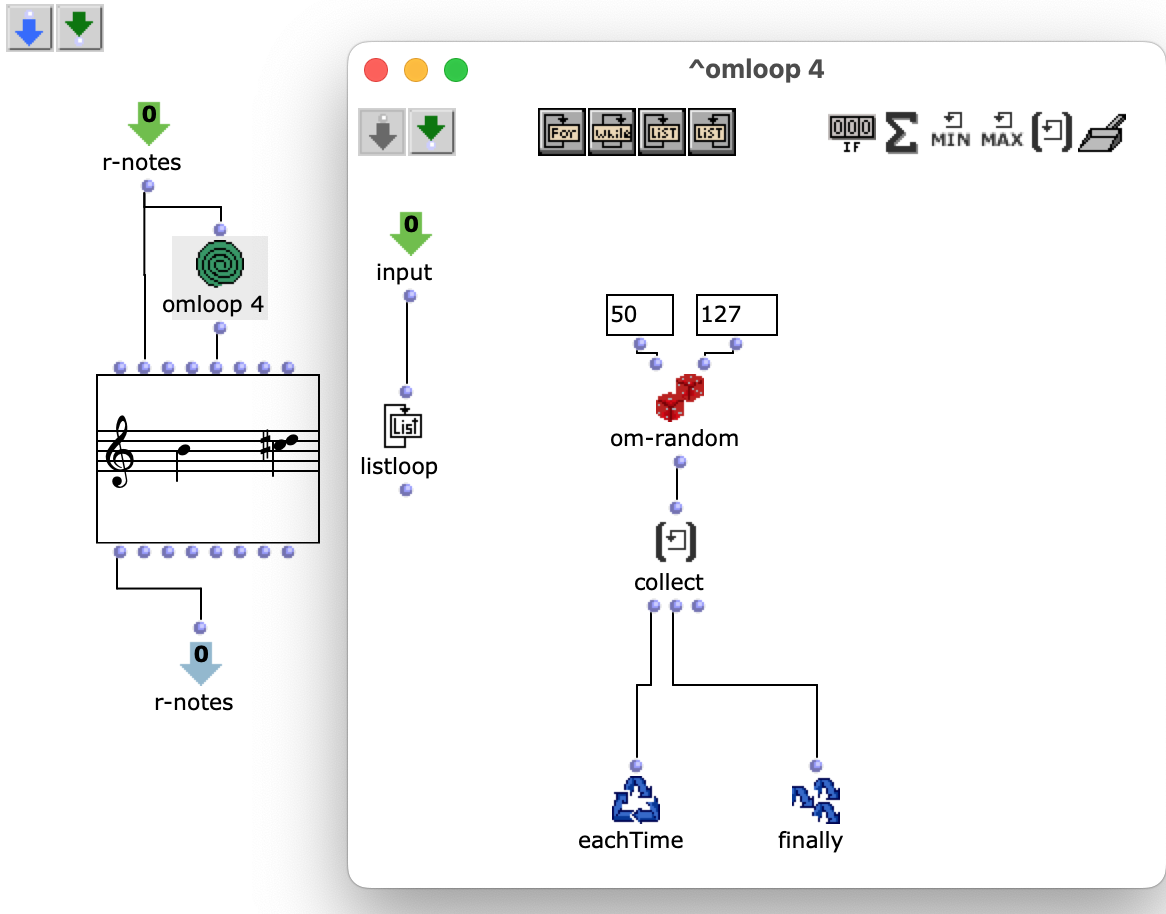
Abb. 6: Erzeugung Dynamik
Abschließend werden die Notenlisten mit ihrem jeweiligen rhythm tree in einem voice Objekt zu einer Stimme verbunden, sodass sich insgesamt drei Stimmen (R, G, B) ergeben, die daraufhin in einem poly Objekt zusammengefasst werden können.
Bildbearbeitung
Um das Klangergebnis zusätzlich zu beeinflussen, besteht die Möglichkeit, die Sättigung der Farbwerte einzelner Bilder der ausgewählten Sequenz zu bearbeiten. Die Originalbilder, werden dann mit den verfremdeten gemischt.
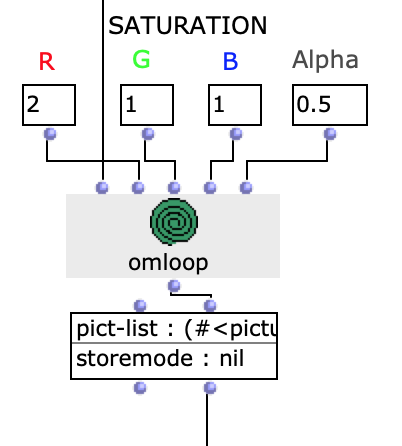
Abb. 7: Veränderung Farbwerte
Beispiel
Im Folgenden habe wurden als Bildsequenz die Frames eines Videos, dass während einer Busfahrt aufgenommen wurde und die Umgebung zeigt, genutzt. Dabei wurde jeder dreißigste Frame abgespeichert. Im Patch wurde dann zudem die Möglichkeit der Farbmanipulation genutzt, um die Sequenz etwas Abwechslungsreicher zu gestalten.

Abb. 8: Bearbeitete Bildsequenz
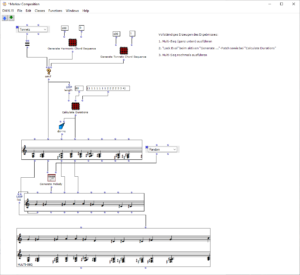
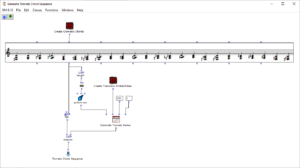
Nach Evaluation des Patches könnte sich ein mögliches Endergebnis dieser Bildsequenz folgendermaßen ansehen und -hören:

Abb. 9: Ausschnitt symbolische Repräsentation